一般相対性理論──数秘術のケーススタディ:スティーブン・クロサーズ
宇宙論が論理的に矛盾し、現実から切り離されている理由
スティーブン・クロサーズ氏の「一般相対性理論──数秘術のケーススタディ」には数式がいっぱい出てきます。私にとってはチンプンカンプンでした。
ソーンヒル氏が「これほど多くの専門家が、ある理論を説明すると称して、これほど多くの本を書き、これほど成功しなかったことはありません」(アインシュタインとは何だったのか?)というアインシュタインの相対性理論。
この相対性理論をスティーブン・クロサーズ氏がどう数学的に料理しているのかということに興味がありました。しかし、時間はかかるし、専門用語が出てきて大変でした。
詳しく知りたい方は、スティーブン・クロサーズ氏の論文「一般相対性理論。ノーベル賞受賞者ヘーラルト・トホーフト教授への謝辞」と「相対性理論と宇宙論 アインシュタインの場の方程式が無効であることの証明。ユニモジュラー欠損の説明」を参照してください。
さて、スティーブン・クロサーズ氏ですが「疑似科学および反科学運動の分析ないし論駁」を目的とした「RationalWiki」の「Stephen J. Crothers」の記事を見ると、面白いことが書かれていました。google翻訳のまま引用します。
私は数学者でも物理学者でもありません。より正確には、私は庭師であり、空き時間に科学を行う家庭の便利屋です。
Stephen J. Crothers (1957–) は、便利屋/庭師であり、パートタイムのアマチュア科学者であり、ブラック ホールは存在せず、一般相対性理論によって予測も互換性もないと主張しています。彼の作品は主に、viXraまたは彼自身の個人的な Web サイトに投稿した記事で構成されているため、査読プロセスを避けています。彼はまた、エレクトリック ユニバースが主催する年次 EU 会議で頻繁にゲスト スピーカーを務めています。
このRationalWikiの記事を読んだ人は、本人が発言したことだと受け取ります。
え? ???なんだろうと思い、調べてみました。
この「私は数学者でも物理学者でもありません……」の出どころは「ブラックホールはどこへ向かうのか?」というサイトの投稿欄です。見ると、三番目に出てきます。
しかも、この文章は「投稿者: Dragonridr 投稿者: KrisFromGenk による投稿への返信」として書かれています。しかし、この投稿は見当たりません。削除されています。
引用された部分は「This does not accurately describe me: I’m neither a mathematician nor a physicist. ……」と書いてあり「これは、私を正確に表現しているわけではありません:私は数学者でも物理学者でもない。……」です。
つまり「私は数学者でも物理学者でもない」以下の文章を「これは、私を正確に表現しているわけではありません」とクロサーズ氏本人が書いているのが分かります。
ところが、RationalWikiの記事は、あたかも「私は数学者でも物理学者でもない」以下の文章をスティーブン・クロサーズ氏本人が書いたかのように記述しています。なんと悪質な。この記事の他の部分も読めば、クロサーズ氏に対する罵詈雑言で溢れていることがわかります。まあ、批判一辺倒で罵詈雑言をする発信者というのは大抵、信用できません。
ここまでして、アインシュタインの相対性理論に対する批判者を貶めたいのでしょうか。残念なことに、このようなことは科学の分野だけに限りません。メディアはソフトに日常的にこれをやっています。

[要旨]
第4回目のカンファレンスEU2015。発見への道 Paths of Discovery で、スティーブン・クロサーズは、名高い一般相対性理論を再検討した。これは、2015年6月29日(月)にフェニックスで発表された彼の講演の全容である。
アルバート・アインシュタインの一般相対性理論は、複雑な数学の入り込めない壁の後ろに隠されており、長い計算をするのが好きな、普通の熊より頭の良い人※だけが理解できるという広範な誤解と重なっている。
※「平均的な熊より賢い」と言われた漫画のキャラクター、ヨギベアにちなんで。
しかし、真実は、そのような講義概要とは大きく異なっている。宇宙論が論理的に矛盾し、現実から切り離されている理由を理解するために数学は必要ないにもかかわらず、主流の宇宙論者は、明らかに誤った独断的信念を正当化して押し付けるために、日常的に数学的神秘主義に頼っている。
数学的な煙(けむに巻くもの)と鏡を見破るために、テンソル計算とその付属品の聖なる秘密が明かされる。高校で習うような微積分の知識があれば、宇宙論者が直面する何よりもギョッとさせる真実であるこの問題に対処する準備は十分に整っている。結局のところ、計算自体は単なる機械的な操作であり、物理学との関連については何も教えてくれない。
不思議なことに、アインシュタインもその追随者たちも正しい計算の仕方を知らなかったことが証明されているので(ヒント:足し算ができない)、この計算を数秘術の一種とみなすのに十分であり、共感呪術(類感呪術 英: Sympathetic magic、Imitative magicは、文化人類学者のジェームズ・フレイザーが定義した、人類学における呪術の性質を表す言葉である。交感魔術、感染[共感、類感]呪術)や骨相学のように、知識の発展を妨げるものである。
スティーブン・J・クロサーズは、オーストラリアのクイーンズランド州を拠点とする著名な数学者であり、すべてを網羅するビッグバン理論を含む宇宙論の標準モデルに対する最も有能な批判者の一人に数えられている。また、ブラックホール理論を体系的に解明し、その数学的モデルが観測からも一般相対性理論からの論理的推論からも導き出されていないことを明らかにした。

00:00 はじめに
02:23 ケーキを焼く⑴
03:38 ケーキを焼く⑵
05:39 ケーキを焼く 4.1
08:34 数秘術101
10:23 ニュートンの当てこすり
12:09 表面理論
17:38 ヒルベルト計量における半径
19:03 シュヴァルツシルトの解法
19:49 ドロステとブリルアンの解法
20:28 シュヴァルツシルトの基本形式
21:14 同等の解決策
21:49 メトリック(計量)拡張?
23:16 ガウス曲率不変量
23:41 クレッチマン・スカラー
29:39 等方性シュヴァルツシルト半径
30:04 等方性シュヴァルツシルトのガウス曲率
30:26 等方性シュヴァルツシルト形式に対する加速度不変量
32:41 シュヴァルツシルト時空のリーマン曲率
32:53 リーマン曲率:シュヴァルツシルト不変量
34:42 別形式の物質がない場合の場の方程式
37:20 混成形式の場の方程式
40:26 微分不変量
42:20 通常の保存則の破れ アインシュタインの場の方程式
44:15 The RIGAs! ──錆びた鉄の銅鑼賞のノミネート作品
スティーブン・クロサーズ:一般相対性理論──数秘術のケーススタディ
Stephen Crothers: General Relativity – a Case Study in Numerology

数秘術のケーススタディ
皆さん、こんにちは。
本日は、EUとサンダーボルト・プロジェクトにお招きいただき、ありがとうございます。
また、私の話に耳を傾けていただきありがとうございます。
さて、私の講演のタイトルは「一般相対性理論:数秘術のケーススタディ」です。これはおどけた意味でもあり、文字通りの意味でもあります。というのも、今日は数学と算数(数字)を使って、一般相対性理論とそれに関連するブラックホールやビッグバンといったものが、実はある種の数秘術にほかならないことをお見せしようと思うからです。

まず始めに、今日の私の話を、亡くなった三人のミュージシャンに捧げたいと思います。
ディープ・パープルのジョン・ロード、そしてサザンロックバンド、アウトローのヒューイ・トマソン・ジュニアとビリー・ジョーンズです。

私と同じか、それ以上の年齢の方なら、きっと覚えていらっしゃるでしょう。
まず、私が好きなことは、ケーキを焼くことから始めることです。さて、どんなケーキでしょう?

ケーキを焼く1
ブラックホールとビッグバンは定義上、相互に排他的である。
| 全てのブラックホール宇宙 | 全てのビッグバン宇宙 |
| ⑴ 空間的に無限、空間的に(κ=1) | ⑴ または空間的に無限(κ=-1, κ=0) |
| ⑵ 永遠の宇宙 | ⑵ 有限の宇宙 (約138億年) |
| ⑶ 質量がひとつしかない | ⑶ 多くの質量と放射を含む |
| ⑷ 膨張していない(静止している) | ⑷ 膨張している(非静止している) |
| ⑸ 漸近的に平坦(または漸近的に曲線) | ⑸ 漸近的に何もない |
| ⑹ k曲率なし | ⑹ k曲率あり |
それは宇宙論的なケーキです。
まず最初に、数学の話に入る前に、少しおさらいをします。
私が過去に話したことは、ブラックホール宇宙──ビッグバン宇宙──の特徴を比較することによって、それらを不可能にしている非常に単純な根本的矛盾を単純に見ることができます。
さて、まず第一に、ブラックホール宇宙は空間的に無限です。
ビッグバン宇宙には三つのタイプがあります。κ曲率の値によって、ひとつは空間的に有限であり、他の二つは空間的に無限です。ブラックホール宇宙は永遠です。つまり、時間に依存しない静的な宇宙なのです。
一方、ビッグバンの宇宙はすべて有限で、138億歳です(現在は、いくつかのノブをいじって139億歳に引き上げられたと思います)。
さて、ブラックホール宇宙は、定義上、ひとつの質量しか持たないものです。しかし、それは私が空に見たものと一致しません。私は少なくとも二つ見ていますし、皆さんも二つ以上見ていることでしょう。
ビッグバン宇宙には、好きなだけ質量があり、放射もあると言われています。すべてのブラックホール宇宙は膨張せず、先ほど言ったように静止しています。しかし、すべてのビッグバン宇宙は非静的です。すべてのブラックホール宇宙は漸近的に平坦です。
宇宙論者によれば、いくつかの難解なタイプは漸近的に曲がっているそうですが、今日はそのような話はしないことにします──それは価値がないからです。しかし、ビッグバン宇宙は漸近的には何もないのです。
最後に、ブラックホール宇宙はκ曲率を持ちませんが、ビッグバン宇宙はすべてκ曲率を持ち、その値は三種類あることが既に分かっています。つまり、ブラックホール宇宙をビッグバン宇宙に入れることはできないし、その逆もできないのです。しかし、宇宙論者はどうするのでしょうか?
この二つを無造作に混ぜると、何百万個、何十億個というブラックホールができます。NASAはそのうちの25億個を発見しました。ESA(欧州宇宙機関)は数日前に天の川でひとつ見つけたばかりです。中心ではなく、別の星と回転しているので、連星系ブラックホールを得たのです。もちろん、これらはすべてビッグバン宇宙での話ですが、ブラックホールも四種類あるので、どれがどれだかわかりません(前回の講演を思い出してください)。
それでは、二番目のケーキを焼くことにしましょう。

ケーキを焼く2
⑴ ブラックホールは分裂病であり、同じ場所(「事象の地平線」)で同時に脱出速度を持ち、かつ持たない。
⑵ ブラックホールの質量は有限であり、無限大の重力を発生させる。
⑶ X=ブラックホール宇宙、Y=ビッグバン宇宙
ブラックホール宇宙とビッグバン宇宙は、非合理的な想像の産物である。
ブラックホールには、非常に分裂的な(矛盾している)性質があります。同じ場所で同時に脱出速度を持ち、同時に脱出速度を持たないのです。さて、脱出速度の意味を理解している宇宙学者はいません。このことは以前の講演で詳しく述べましたが、今日はそのおさらいです。だから、それが問題なのです。
脱出速度のあるものとないものが同じ場所に同時に存在することはありません。しかし、それはまさにブラックホールの事象の地平線が持っているものです。実際、ブラックホールの事象の地平線の脱出速度、あるいは事象の地平線のブラックホールの脱出速度が光速であることを教えてくれています。だから、何も逃げることができないのです。そうなんですか?
もし光が光速で進んでいて、それが光の脱出速度なら、光は逃げられると思いませんか?
そうです。続けて、Xはブラックホール宇宙、Yはビッグバン宇宙としましょう。
X+Yは宇宙ではありません。
X+XもY+Yもない。
なぜでしょう?
一般相対性理論は非線形理論なので、単純な方程式の解のように、これらを足し合わせることはできません。非線形理論なので、そんなことはできません。ここでは、ブラックホールの簡単なグラフィックス例を示します。

ケーキを焼く3
すべての’ブラックホール’は、他のすべての’ブラックホール’において無限の重力に遭遇する。
これらのホールはどれも漸近的には何もない! 矛盾している(誇大な宣伝に反する、反対意見宣伝?)!
一般相対性理論や宇宙論によれば、すべてのブラックホールはその特異点において無限の曲率を持ちます。もし、すべての特異点で無限の曲率を持つなら、それは重力となります。一般相対性理論では重力は力ではなく、時空間曲率です。
つまり、これらのブラックホール(そこにある小さな絵を見てください)の一つひとつは、その中心、いわゆる特異点で無限の曲率を持っていると言っています。しかし、そのどれもが漸近的な平坦性を持っているのでしょうか?
さて、あるブラックホールから別のブラックホールへ行くと、何が起こるでしょうか?
無限の重力です。別のブラックホールから別のブラックホールへ行くと、無限大の重力があります。すべてのブラックホールは、他のすべてのブラックホールで無限の重力に遭遇します。それは漸近的なものではなく、ブラックホール宇宙の定義に反しています。少なくとも漸近的に平坦であるはずなので、ナンセンスです。
さて、ここからは少し数学的な話になります。
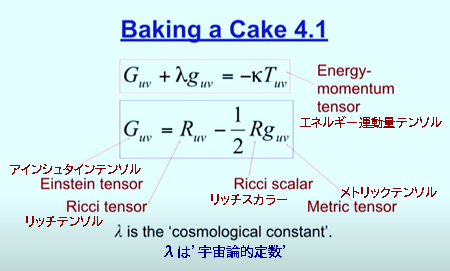
ケーキを焼く 4.1
アインシュタインテンソル、リッチテンソル、リッチスカラー、メトリックテンソル、エネルギー運動量テンソル、λは’宇宙論的定数’
ケーキを焼く4.1まで来ましたが、誰のケーキを焼いているのでしょう?
さて、宇宙論者のケーキとアインシュタインのケーキ、本当はどこかにファイルが欲しいところでしょう……
私は彼らに特権を与えるつもりはありません。
さて、一般相対性理論。これはアインシュタインの方程式です。さて、ここで本当に必要なのは、要素を特定することです。
'G’──この大文字のGは何ですか?
アインシュタインテンソルです。
'R’はRuvで、これはリッチテンソルです。
Rはリッチテンソル Ricci tensor から派生したもので、リッチスカラー Ricci scalar と呼ばれます。そして’g’、これはメトリックテンソルと呼ばれる重要なもので、基本テンソルと呼ばれることもあります。メトリックスについて説明しましょう。そして(ラムダ)λ は宇宙定数、’T’はエネルギー運動量テンソルです。以上です。
我々はすべての要素を特定しましたが、それらは何を意味するのでしょうか?
エネルギー運動量テンソルは、アインシュタインの重力場のすべての物質的な原因を記述することになっています。そしてGは幾何学を記述することになっています。物質が時空を湾曲させるからです。つまり、右側にある物質が左側にある時空を曲げているのです。それがアインシュタインの言う重力です。
宇宙定数とは何でしょうか?
宇宙論者はよく知りません。アインシュタインもよく分かっていない。ファッジファクター(補正係数、目的の結果を生成するためにその場しのぎの方法で変更される値またはパラメーター)なんです。
ここで興味深いことがあります。
静的で、物質がない場合、(アインシュタインによれば)エネルギー運動量テンソル(前のスライドで見た)がゼロのとき、彼の方程式は次のものに帰結します:リッチテンソルRuv=0です。さて、アインシュタインによれば、これは星のような物体の外側の重力場を記述しています。しかし、これは循環論法です。
まず、エネルギー運動量テンソルをゼロにすることによって、すべての物質を取り除く。そして、一周して戻ってくると、これは物体の外側の重力場を記述するもので、彼はそれを元に戻しただけなのだ、と言う。
さて、一部の人々は、クロサーズは知らない、間違った道を進んでいる、と反論するでしょう。そうでもないのです。ここで、ド・ジッター宇宙を例にとると、R=λGという二番目の方程式で記述されるので、この議論が循環していることが証明できます。宇宙論者やアインシュタインによれば、この宇宙は空っぽです。ド・ジッターの空宇宙ですよね?
何も入っていないので、空っぽです。なぜ何も入っていないのでしょうか?
エネルギー運動量テンソルがゼロだからです。さっきのと同じですね。つまり、アインシュタインとその信奉者によれば、まさに同じ数学的制約によって、物質は存在し、かつ存在しないことになるのです。そんなことが可能だと思いますか?
思わない。ありえない。

ケーキを焼く 4.2
物質源は、同じ数学的制約、Tuv=0によって、存在も不在もある!
アインシュタインのケーキが焼き上がった。
つまり、リッチテンソルはゼロに等しく、その宇宙は、もし宇宙であるなら、ド・ジッターの宇宙と同じ理由で空っぽなのです──物質的な源が存在しないのです。これは矛盾です。アインシュタインのケーキは、これで完全に焼き上がったわけです。これについては後で詳しく述べますが、つまり、リッチテンソルをゼロにすることは物理的に無意味であり、物理とは何の関係もありません。

数秘術入門
'シュヴァルツシルトの解’:ヒルベルトのマジック!
ここからブラックホールは最初から完全に失敗した。
さて、ここで少し数秘術(数秘学、数霊術、数理神秘学、数字占い)の話になります。
これはいわゆるシュヴァルツシルト解ですが、ヒルベルトのバージョンで、ヒルベルトの手品です。
この式では、c=G=1
cって何ですか?
それは光の速さです。
Gはニュートンの重力定数で、それらを1に設定することで方程式から消え、この方程式の中のこの小さな’m’が、アインシュタインがリッチイコール無と言っている重力場の質量(源)だと主張しているのです。これは、取り出され、戻された謎の質量です。
この式にニュートンをどう組み込むか見てみましょう。’c’と’G’を明示的に入れてみましょう。

ニュートンのほのめかし
'シュヴァルツシルト半径’は、
ゆえに、 脱出速度!
ここで、ヒルベルトの式は次のようになります。cとGが存在するのは、cとGを1にするとヒルベルトの2m/Rが得られるからです、彼らは’R’が0になることを望んでいることに気がつく。これによって、二つのいわゆる特異点ができます。Rがいわゆるシュヴァルツシルト半径に等しいとき、彼らはそれを半径と呼び、2Gm/c²に値を与えるので、ブラックホールの事象の地平線を取り除くことができると言うのです。ここでも、Gとc=1とすると、R=2mとなり、これをこの式に当てはめると、第2項の−1乗は、1/0となることがわかります。そうでしょう?
これは未定義なので、彼らはこれを「事象の地平線 event horizon」と呼んでいます。
次に、Rをゼロにしたいから r=0を入れ(彼らはそれが半径だと考えている)、0を入れると、第1項はどうなりますか?
1/0となる。
さて、このいわゆるシュヴァルツシルト方程式、つまりシュヴァルツシルト半径をcについて並べ替えると、c=√2Gm/rs となることに気がつきます。それで、この式はニュートンの脱出速度の式であることはすぐにわかります。もちろん、ニュートンの脱出速度の式は二つの物体に適用されるものです。ひとつの物体がもう一つの物体から逃げるのだから、少なくとも二つの物体がなければならない。
この方程式から質量がひとつ欠けたからといって、それが暗黙のうちに存在しないことにはなりません。なぜなら、二つのものがあり、一方は他方から逃げていくからです。これは、ある物体が別の物体から逃げるのに必要な最小の速度は何かということを説明しています。その物体は質量’m’を持っています。
つまり、この表現によって、彼らは二つのものを持っていることになります。
1. ブラックホールの事象の地平線の半径と、
2. ブラックホールの脱出速度です。
事象の地平線の脱出速度が光速であることは、ニュートンの式から得たものです。
一体の問題の解とされるものに、どうして二体の関係を入れることができるのでしょうか?
それは無理です。ここで、さらに混乱が生じます。

混迷する宇宙論者たち
ヒルベルトの’r’は
⑴ 面的半径
⑵ 座標半径
⑶ 半径(例:ヘーラルト・トホーフト、ノーベル賞受賞者)
⑷ 距離(例:ヘーラルト・トホーフト、ノーベル賞受賞者)
⑸ 半径座標(例:ヘーラルト・トホーフト、ノーベル賞受賞者)
⑹ 2球の半径
⑺ 縮小円周率
⑻ 半径空間座標。
⑼ ゲージ選択;座標 r を定義する(ヘーラルト・トホーフト、ノーベル賞受賞者)
これが科学的というか妄想的な科学というか。妄想科学、混乱する宇宙論者たち。ヒルベルトの’r’を何だと思ってるんでしょう?
私たちはその式を見ました。
⑴ 面積半径 ⑵ 座標半径 ⑶ 半径──ノーベル賞を受賞したヘーラルト・トホーフト Gerardus 't Hooft という人が教えてくれたのですが、これは半径なのです。彼はまた、⑷ 距離だと言っていますし、他の多くの人も言っています。⑸ 半径座標だと言っていますし、他の多くの人も言っています。⑹ 二球面(?二重球)の半径、⑺ 縮小円周、⑻ 半径空間座標、そして私のお気に入りのものは ⑼ ゲージ選択──これは座標’r’を定義しています。
そして、これを"フレッド・フリントストーン(原始家族フリントストーン、アメリカ製テレビアニメ)“と呼ぶこともできるし、"ダークマター"と呼ぶこともできるし、"どうでもいい"と呼ぶこともでます。そんなことはどうでもいいのです!
[会場笑]
なぜなら、それらすべてが間違っているからです!
では、なぜ彼らの数学が間違っているのかを知るために、少し表面理論に迫ります。

表面理論
第一基本二次形式
これは簡単な式で、面の第一基本二次形式と呼ばれます。
さて、gは2変数、uとvの関数です。uとvが唯一の変数であり、ここでいくつかの項、guuguvgvvを持っていることがわかります。まあ、guv=gvu──だから二回出てくる。しかし、変数はいくつあるのでしょうか?
二つです。これは曲面だからです。表面には二つの変数、二次元しかない。面積は、ガウスの表面理論から、二番目の式で書かれた面積の要素で与えられます。これは面積の要素であり、これを積分して、必要なuとvの値に対する領域の範囲に渡って、完全な面積を得る必要があります。
さて、uとvが別のパラメータの関数である場合、それを’t’と呼ぶことにします。しかし、’t’と呼ぶからといって、それが '時間’であるとは限らない。ここでも、フレッド・フリントストーン、uの関数として、フレッド・フリントストーンを入れることができました。そこに貼り付けることができます。そして、表面のどこにでも長さのある要素を得ることができます。このパラメータ化された式によって、その表面の二点間の長さを計算することができます──パラメータを使うために。呼び方はどうでもよくて、ただのダミー変数です。

行列としての計量テンソル
表面のメトリックテンソル
表面のメトリックテンソルの決定要素
計量テンソル Metric tensors。
これは宇宙論者が隠していることがたくさんあります。ほとんどの人はそれを理解していません──彼らは、ああ、これはテンソルだね、と言います。
そうなんですか?
テンソルってなんですか?
ほとんどの人はそれすら知らないのに、それでも使っている。教科書を読んでこよう。
計量テンソル。
えーと、前に見たのは、g、u、vがありました。さて、四つ全部をカバーする g₁₁, g₁₂, g₂₁, g₂₂ があればいいんです。最初の一つ、真ん中の二つ、そして三つ目、つまり表面なので、ここには四つの成分しかないのです。そして、これらをまとめてこのような行列に書くことができます。これを計量テンソルと呼びます。そして、この計量テンソルの決定要素(?決定要因)は、単に決定要素を取るだけです。決定要因の理論では、これの決定要因を取るのですが、これはとても簡単です。gは決定要因を表し、guvは行列として書けるので、guvは計量テンソルと呼ぶことにします。
でも、計量ってなんでしょう?
線要素と呼ばれることもあります。線要素ってなんですか?
それは距離の公式の空想上の名前に他なりません。この二つの点の違いは何ですか?
式を書いてくれ。どうやって計算するんですか?
計算式を教えてください。初等代数学や解析幾何学では、10年生(15~16歳)で習います。
二つの点があります。X1, Y1 と X2, Y2 があります。この二点間の距離は?
ピタゴラスの定理を適用して、距離を求めます。さて、少しずつやっていくと、線の要素、つまり距離の公式が得られます。では、特に距離の公式を見てみましょう。OK。

ガウス曲率
表面の本質的な幾何学は、どのような埋め込み空間にも全く依存しない。
ヒルベルト計量における表面は、
そのガウス曲率κは次のように計算される
ここでガウス曲率というものを計算したいのですが、これはヒルベルト計量における’r’が何であるかを特定し、それがゼロになるかどうかを確認するためです。
これから、それがゼロにならないことをお見せします。そのため、ブラックホールに関するすべてのことが直ちに破壊されます。表面の内在的な(固有の、本質的な)幾何学は、どんな埋め込み空間にも全く依存しないので、二次元である表面を三次元空間(どんな空間でもいい)に貼り付けても、表面の内在的幾何学は変化しません。つまり、埋め込み空間を全く無視して表面の内在的幾何学について語ることできます。必要ないのです。ガウスはそれを証明しました。
さて、ヒルベルトの解、ヒルベルトの計量における表面は、これ : ds² です。変数θ (Theta) とφ (phi) の二つだけであることがわかります。ここでは’r’は変数ではなく、’dr’もありません。’r’は固定量であり、何らかの値を割り当てることができます。
さて、表面のガウス曲率を計算する場合、κ = R₁₂₁₂/gでできます。’g’は前に見たように計量テンソルの決定要因で、’r’は何でしょう?
これは第一種のリーマン・テンソルの成分です。そのことには触れません、そういうものだと知っていればいいのです。
それから、’g’は何でしょう?
さて、この場合、g₁₁ は何でしょう?
r²です。g₁₂₂₁ は出てこないからゼロ、g₂₂ は r²sin²θ、つまり変数の係数なんです。これはどうやって計算するのでしょうか?

ヒルベルトの’r’の正体
つまり、ガウス曲率は
さて、私たちは(いくつもの方法がありますが、ここではより簡単な方法を紹介します)(?目的語が抜けている)を使って計算する必要があります。

ちょっと戻りますが、この計量テンソルを見ると、左上に r²、右上に r²sin²θ がありますね、これは対角線です。対角線上以外の場所にゼロがある場合、これは対角行列と呼ばれます。つまり、この計量テンソルは対角行列であると言えます。──数学の専門用語です。さて、対角テンソルの場合、これらの簡単な関係を使って、ガウス曲率を計算することができます。

上の式は第二種のリーマン・テンソル、二番目の式は第一種のリーマン・テンソル、そして前に見た1212ビットをどう得るかを示しています。
さて、これらの他のもの、Γ(ガンマ)記号を計算するために、これらはリーマン・クリストッフェル記号と呼ばれ、複雑なものですが、これらを計算するために、これら二つの関係式があります。
さて、これらの計算をすべて行った場合、私たちが欲しい結果、集中したい結果は一番下のものです。ガウス曲率は1/r²となります。これで、ヒルベルトの計量における’r’が何であるかがわかりました。宇宙論者が言っているようなことは何もありません。
'r’とは何か?
ガウス曲率に関連していて、この場合、表面のガウス曲率の逆平方根です。もちろん、表面形状(表面幾何構造)は、埋め込み空間に依存しないので、埋め込み空間に曲面を貼り付けるわけですね?
その場合でも、同一性は変わりません。ヒルベルトの計量における実半径は?
計算をして、’r’を含む項を積分し、定数を評価すると、このような式が得られます。

ヒルベルト計量における半径は
定数を入れると、第二項は√αになります。
ここで、r=α のとき、ヒルベルトの場合、α=2Gm/c²を与えて、cとG=1 にして、Rp=0、これが半径になることに注目してください。つまり、r=α、ヒルベルトの場合は 2Gm/c²のとき、この式はゼロになります。半径方向の距離はゼロになります。ということは、この幾何学の原点はそこにあり、0≦rの可能性はないのです。
ミンコフスキーの計量を見てみましょう。

ミンコフスキーの計量 (SR)
半径は、
ガウス曲率は、
これは特殊相対性理論、つまり平坦な時空のための計量です。r = 0 まで下がります。半径を計算すると、Rp = r となります。両者は同じです。もう一方に戻ると、Rp = r となるでしょうか?
いいえ、非ユークリッド幾何学なので、半径を計算すると、それは別物です。この場合、ガウス曲率と半径は、このような形で直接関係します。1/r²はガウス曲率であり、’r’は半径でもある。ということが、計算でわかるのです。なんで?
ユークリッド空間だからであって、もう一方は非ユークリッド空間だから、同じ関係にはないのです。だから、ガウス曲率は 1/r²なのです。
シュヴァルツシルトの解を見てみましょう、ヒルベルトの解に似ていますね。

シュヴァルツシルトの解
ヒルベルトの解は、シュヴァルツシルトの解と等価ではない
この場合、シュヴァルツシルトの’r’は0になります。しかし、彼の r=0 の時、彼の’R’はどうなるのでしょうか?
彼の R=α は、まさに私が話してきた定数です。そうでしょう?
したがって、ヒルベルトの解はシュヴァルツシルトの解と等価ではありません。なぜなら、もしそうなら、シュヴァルツシルトの’R’は-α まで下がる必要があるが、それはありえないからです。r ≥ 0 で定義されています。
ドロステの解を見てみましょう。

ドロステとブリルアンの解
ドロステの解
ブリルアンの解
これはヒルベルトの解とそっくりですが、2mではなくα があるのが異なります。また、α≦r で、ここでも c=1 です。
そして、ブリルアンの解との比較です。ブリルアンはこの方程式を1923年に書きましたが、彼の場合、0 ≤ r ですが、’r’は現在では(一種の)パラメーターのように作用しています。ds²はこれ、0≤r です。どうでしょう?
この二つは等価で、シュヴァルツシルトの r=0 のとき、それはドロステの r=α のときと同じで、さらにブリルアンの r=0 のときと同じだからです。どれも同じように、半径が0になることを演出しています。宇宙論者がやりたいことは、α≦r のドロステの解をとって、’r’をゼロにすることです。なぜでしょうか?
なぜなら、彼らはそれが半径だと考えているからです。そうでないことはもうわかりました。そして、彼らは、r=0 を幾何学の原点としたいのだが、そうではない。
シュヴァルツシルトの基本形式を見てみましょう。

シュヴァルツシルトの基本形式
等価な解の無限集合
これは私が2005年に書き留めたもので、このテーマに関する最初の論文です。この式を見てください。特に、Rc 。ここで、’n’は任意の正の実数、’r’は任意の実数であることがわかります。r₀も、任意の実数です。
r0 と’n’は任意の定数で、好きなものを選べます。しかし、あることに気づいてください。r = r0の時、前に計算した半径は常にゼロで、’n’と’r0'の値とは独立しています。完全に独立している、これがあなたが欲しいもの、座標の独立性です。つまり、Rc=α Rp (r0)=0 は、すべての r0 の値とすべての’n’の値に対して成り立つことが分かります。いくつか例を挙げてみよう。

等価解の設定
ドロステの解を0≦rに拡張してヒルベルトの解(つまりブラックホール)を作ることができるだろうか?
いいえ、できない!
シュヴァルツシルトがやったように、r0=0、n=3、r>r0とすると、シュヴァルツシルトの解が得られます。
n=1、r0=α、r>r0とすると、ドロステの解が得られます。
n=1、r0=0、r>r0とすると、ブリルアンの解が得られます。
これらの方程式は等価です。幾何学的に全く同じであることを、記号が違うだけで同じことを言っています。
そこで問題です。ドロステの解を無に拡張してヒルベルトの解を求め、ブラックホールを生成することは可能か?
さて、ここで計量拡張の話をします。さて、ここで、もしあなたがそれを見ることができなかったら、そんなことはできないことをお見せしましょう。

メトリックの拡張は?
したがって、どれも’拡張’することはできない。
ブラックホールは存在しない。
具体的な例として、Rc の式で r0=0 とし、n=2 とします。
どうなるでしょうか?
この式は Rc = (r²+α²)½ です。
さて、’r’は実数で、実数を二乗すると別の実数が得られますが、この二乗した実数は常に≥0であるという違いがあります。
r²は−α(マイナスアルファー)を取ることができるか。
r²は−αになれるか?
それはできません。
さて、この式はシュヴァルツシルトの解、ドロステの解、ブリルアンの解、好きな数の解を生成し、それらはすべて等価です。もしその無限の等価クラスのどれかが、ヒルベルトのブラックホールを作る(言い換えれば、ドロステの解を無にする)ために拡張可能なら、それらのすべてが等価であるはずです。あるいは、逆に、その中のひとつでも Rc=0 にできないものがあれば、等価のゆえに、どれもできないことになります。
さて、これを見ると、r²がマイナスαの値をとって、Rc=0 にすることができるかというと、できません。つまり、同相(同相写像、位相同形)も微分同相写像もハウスドルフ空間も位相空間も必要ありません。これでは、単純な数学でブラックホールが完全にダメになってしまいます。同値類(等価クラス)だからできないのです。
今、あることにも気づいてください、Rc を作ると、r=r0は必ず α になるのです。

ガウス曲率不変
これは正有限不変である。
つまり、これらの解のガウス曲率は常にこの値:1/α²──どんな r0 を選んでも、どんな’n’を選んでも、それはシュヴァルツシルトの、ドロステの、ブリルアンの、すべての、しかしヒルベルトの、そこにはないものなのです。なぜか?
それは、この幾何学から完全に切り離されているからです。つまり、ブラックホールはどこにもできないし、ブラックホールが生まれたのはヒルベルトの解からです。
曲率については、クレッチマン・スカラー(これはリーマン・スカラー曲率不変量と呼ばれることもあります)のことが話題になります。

クレッチマン・スカラー
シュヴァルツシルト形式の場合は、
これは常に有限であり、不変である。
さて、シュヴァルツシルトの時空の場合、それは’ ⨍ 'で与えられ、ここで、すべての r0 とすべての’n’に対して ⨍(r0)=12/α⁴が示されていることがわかります。なぜか?
それは無限の同値類だからです。
12/0を求めることができるのでしょうか?
' ⨍ 'の分母がゼロになることはあるのでしょうか?
いいえ。
だから、分母を0にできるという彼らの主張は誤りです。
加速度不変と呼ばれるものを見てみましょう。

加速度不変
シュヴァルツシルト時空における’点’の半径方向の測地線加速度は、次式で与えられる
これは不変条件である。
これは幾何学なので、点の話をします──動く点です。
さて、このような物理的には何の意味もないシュヴァルツシルト空間における点の半径方向の測地加速度を求める式は、これまで見てきたように、この式で与えられることを、ドウティはずっと以前に証明しました(あるいはずっと以前に示した)。そして今、私の Rc を入れると、それは同値類、無限同値類なので全てに有効で、(r → r0) (Rc → α) の時、加速度はどうなるでしょうか?
いくらでも大きくなります!
ということは、これは、どの r0を選んでも、どの’n’を選んでも同じということです。
さて、宇宙論者によれば、今度は物質のないところで、無限に近い加速度が得られるということです。彼らは、クルスカル・スゼッケル’座標’と呼ばれる空想的なものを使って、ドロステの解を r=0 に追いやろうとします。

クルスカル・スゼッケル’座標'
これは、Rc=0には拡張されない。
もう一度言うが、ブラックホールはおとぎ話だ。
ここにも書きましたが、クルスカル・スゼッケルの’座標’は、Rc を使った線要素、つまり計量であり、それが無限の同値類(等価クラス)を生成するものであるからです。Rc が0になることはありえないことがわかりますか?
絶対にありません!
では、Rc をゼロまで拡張することができるのでしょうか?
いいえ、できません。
だから、この拡張はおとぎ話です。できないのです。さて、これでブラックホールにまつわるすべての道具一式(複雑な手続き、不要なもの)が停止しました。
では、四つのブラックホールを見てみましょう。

概論
シュヴァルツシルトの’ブラックホール’:- 電荷は中立で、回転しない。
ライスナー・ノルトストレムの’ブラックホール’:- 電荷があり、回転しない。
カー 'ブラックホール’:- 電荷は中性で、回転する。
カー-ニューマン 'ブラックホール’:- 電荷があり、回転する。
全体的な基本形式は?
シュヴァルツシルトのブラックホールから、ある方法でこれらを生成することができます。シュヴァルツシルトのブラックホールは、あるいは"ブラックホールとされるもの"は、荷電しておらず中立で、回転しません。
ライスナー・ノルドシュトロム(ライスナー-ノルドシュトロム・ブラック ホールは、質量と電荷を持つブラック ホールだが、スピンはない)は帯電しており、回転はありません。
カー["ブラックホール"は電荷が中性で回転する]そして、カー-ニューマン"ブラックホール"は電荷があり、回転します。
何が回転しているのか?
彼らによると、点または円周です。さて、ここでそのすべてを説明するつもりはありませんが、全体的な基本形は以下の通りです。

全てを含めた計量基本形式
等価解の無限集合は次式で与えられる
私はずいぶん前にこれを書きましたが、私の評論家の誰も、もちろんそれに気づきもしませんでした。もちろん、誰一人として理解していません。でも、本当に簡単なことです。ここに Rc と書いてあるのは、一般化されています。今、すべてのブラックホール(とされている’ブラックホール’)は、必要なパラメータを選択するだけで、この式に含まれます。
さて、ここで Rc(r0)=σ がわかりますが、σ の式で σ は2乗された電荷’q’、2乗された角運動量’a’を持つようになりました。しかし、Rc (r0)=σ は、すべての r0とすべての’n’について、そうでなければならないのです。
rc が0になることはないのでしょうか?
Rc を見ると、0になることはない。σ より小さい値をとることはありません。
さて、q=0、α=0 とすると、σ は α に正確に低減します──これがシュヴァルツシルトのものです──回転もなく、電荷もない。まさに私たちが必要としているものです。それで…… これは拡張不可能であるという理由で、どれも不可能なのです。

拡張可能なものはない
r2は負の値をとることができない。 ブラックホールは誤謬(誤った推論)である。
だから、ブラックホールは誤りなのです。
物理学とは無関係の無意味な数学と結びついた非合理的な想像力の産物以外の何物でもありません。アインシュタインの場の方程式は Ricci、つまりRuv=0であり、物理的な意味はないのです。
ここで、全部のガウス曲率について私が得た式を示します。

全部のガウス曲率
これは球対称ではないが、以下のよう縮小される。
さて、これが非常に複雑な式であることはおわかりいただけると思います。
さて、球面とは何でしょうか?
さて、純粋数学者によれば、一定の正のガウス曲率を持つ曲面はすべて球面です。この式を見てみると、正でもなく、一定でもない。
なぜか?
なぜなら、それは球形ではないということだからです。
しかし、ここで α=0 ではなく、角運動量を a=0 とすると、球面に帰着します。q=0、a=0 にすると 1/α²になります。これはシュヴァルツシルトの、時空のシュヴァルツシルトにおける表面のガウス曲率です。この式は、それらをすべて網羅しています。どれも、ブラックホールの発生を許さない。
さて、ここでクレッチマン・スカラー全体の複雑な表現があります。

全てを含めたクレッチマン・スカラー
これは常に有限である。
もう一度言いますが、Rc を最も一般的な形で使ってみると(前のスライドにあります)、この式は決して 1/∞ではないことがわかります。つまり、ゼロになる量に対して1であると言うでしょう。もう一度言いますが、分母が0になることはありません。常に正の有限値なので、ブラックホールの中心で曲率が無限大になることをクレッチマン・スカラーに頼るのは、まったくもってナンセンスです。中には、これらの方程式を等方性座標と呼ばれるもので書いて、さらに混乱させようとする人もいます。

等方性シュヴァルツシルト基本形式
ここで、私が昔開発した等方性座標の式を紹介しましょう。さて、この二つの形式は球対称性に関連していることがわかると思います。この式は、違う形をしているのがわかります。(α/4)nが出てきました。
なぜでしょうか?
なぜなら、等方性座標──右側の4の累乗の部分の式を見てください、これはユークリッド三空間の式に他なりません。つまり、このように書き直すと、これが等方性座標と呼ばれるもので、その意味はそれだけです。
さて、等方性座標で半径を計算すると、半径 Rc はこれ、Rp は r0、その半径は無に等しいと出ます。

等方性シュヴァルツシルト半径
'ブラックホール’は存在しない。
そして、r0 のどの値を選んでも、’n’のどの値を選んでもいいのです──完全に独立しています──無限の同値類が生成され、そのどれもがブラックホールには拡張できず、同値性の理由から、そこ(ブラックホール)には何も行かせられないのです。
等方性シュヴァルツシルト・ガウス曲率。
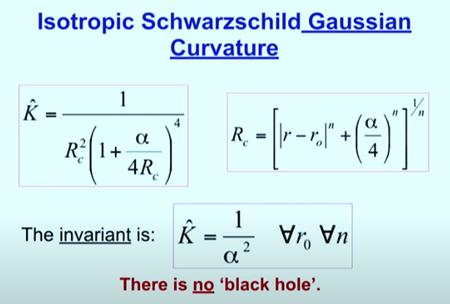
等方性シュヴァルツシルト・ガウス曲率
不変式は:
'ブラックホール’は存在しない。
計算すると、シュヴァルツシルトの場合と全く同じになります。なぜなら、ここでは等方的なシュヴァルツシルト時空を扱っているからです。さて、これを普通の形に置き換えると、やはり全く同じガウス曲率が得られます、そうでなければならないのです!
結局のところ、等価なのです。クラスは違いますが、等価であることに変わりはないのです。加速度不変は、まったく同じ性質を持っていることがわかりました。

等方性シュヴァルツシルト形式の加速度不変
したがって、ブラックホールは存在しない!
しかし、事象の地平線がそこにあると言いますが、やはり、加速度は無限大に広がり、そこには物質が存在しないと言うのです。ひとつだけ、リーマン曲率の計算をしたことがないのは、おそらく彼らにとって複雑すぎるからでしょう。そこで、私はわざわざそれをやってみました。

リーマン曲率
ガウス曲率を二次元以上に一般化。
これで、私が言ったことがすべて補強されました。
リーマン曲率はどのように計算するのですか?
さて、ここにこんなものがあります。分数の分子には(分子にあるのは)Rijkl があり、これは第一種のリーマン・テンソルとして知られています。’U’と’V’は方向ベクトルです。つまり、ある点を取ってそこに二つのベクトルを置くと、好きな方向に向けることができます。つまり、曲率は位置だけでなく、そこにつけた方向ベクトルにも依存することがわかりますね?
二次元空間の場合、球面対称性(シュヴァルツシルトのときのもの)では、これは 1/r²に縮まります。
さて、非球面空間では…… そう、球面空間では、やはり同じように、これを使って計算します…… 非球面空間は本当に複雑になります。どうせ意味ないからいいんだけど、面倒くさいからやめておきましょう。
では、どのように計算するのか?
'U’と’V’は方向ベクトル、’r’は分かっている、’g’はそこで与えられた計量テンソルの成分で定義される、といったところでしょうか。
定義を述べます。私が作ったのではありません、数学者たちが作ったのです。私は数学者から借りただけで、彼らが使うようにと言ったものを使っています。私は数学者が正しくやったと信じていますが、時にはそうでないこともあります。

等方点:
定義:ある点でのリーマン湾曲がその点での方向ベクトルに依存しない場合、その点は等方点と呼ばれる。
とにかく、定義:もし、ある点でのリーマン曲率がその点での方向ベクトルに依存しないなら、その点は等方点と呼ばれる。
なぜか?
それは、どこでも同じということです。方向ベクトルとは無関係です。
ここで、シュヴァルツシルト時空の残りの曲率について計算してみましょう。

シュヴァルツシルト時空のリーマン曲率
Rc はそのままで、’r’は実数、’n’は任意の正の実数、’W’は二つの行列式からなり、方向ベクトルに関係する二つの行列式の積であることがわかります。右の項は、分子も分母も非常に複雑です。というわけで、今結果を示しましたが、正しいかどうか確認したい場合は、いつでも戻って確認することができます。どこかに間違いがあるかもしれませんが、その時は教えてください。私はそうしていますし、間違いもあります。誰にでも間違いはありますから。宇宙論者は間違いを犯すと、まあいいや、先に進もう……と言ってしまうのです。
リーマン曲率、シュヴァルツシルト不変量。

リーマン曲率、シュヴァルツシルト不変量
r0 は等方的な点になる。
さて、シュヴァルツシルト時空のリーマン曲率を計算すると、Ks が得られます。これから’s’をつけて、ガウス曲率ではなくリーマン曲率について説明します。このリーマン曲率は4変数全体に適用されますが、以前は2変数の表面について話していました。
さて,このシュヴァルツシルト空間のすべてを,私が一般化した形で生成してみると(シュヴァルツシルト,ドロステ,ブリルアン,それらすべてを含む)──ヒルベルトのものではない、なぜならヒルベルトのものは等価ではないのだから──それで 1/2α²が得られます。これは有限であり、不変です。これは、r0と’n’のどのような選択に対しても同じです。

等方的なシュヴァルツシルト時空のリーマン曲率
シュヴァルツシルト時空の等方性座標でも、もっと複雑な式でも、同じことができます。
なぜか?
今は等方座標なので、Ks は別の式になり、計算するとこうなります。1/2α²。

リーマン曲率:等方性シュヴァルツシルト不変量
なぜか?
シュヴァルツシルト空間だからです。曲率が同じでないと不変量にならないんです。
この計算を確認したいのなら、私は100ページの論文を書きました。60ページは付録(別表)と数学で、40ページは、この数学のすべてに通じているわけではありませんが、少なくとも学びたい人にはかなり読みやすいものです。

全計算結果
クロサーズ、S.J.、一般相対性理論。ノーベル賞受賞者 ヘーラルト・トホーフト教授への謝辞, https://vixra.org/pdf/1409.0072v6.pdf
この論文は、ヘーラルト・トホーフト教授への謝辞のようなもので、彼の批判に答える機会として、最高の銀色の大皿を与えてくれたのです。というわけで、そこに行きたいというなら、そこにあります。不快な(厄介な)細部はすべてそこにあり(付録)、すべての計算を経て、それがどのように得られたかを見ることができます。
さて、アインシュタインの場の方程式を別の形で書いてみましょう。

別の形の物質が存在しない場合の場の方程式
アインシュタインはこのように書きました。リッチテンソルがゼロになる前は、このように書いていました。これは違う形です。リーマン-クリストッフェル記号で言うと、左辺は幾何学、右辺はソースがなく、既知数の負の平方根は1になることがわかりました。
なぜか?
シュヴァルツシルト計量など、この計量値の決定数を取ると、−1、つまり負の数が得られるので、正の数の平方根を得るには、−1を掛けなければなりません。アインシュタインはこの、いわゆるユニモジュラー・シュチュエーションを設定しました。宇宙論者は「これは単峰性(度数分布を表すグラフにおいて、峰が一つだけある)座標だ、だから彼はそうしたんだ」と言うでしょう。
だから何ですか!?
さて、アインシュタインはリーマン-クリストッフェルの記号に手を加えています。前にマイナスをつけて、上の方程式をプラス記号で書けるようにしています。気をつけなければならないのは、アインシュタインを読むと符号が分からなくなることがあります。

混合形式の物質がない場合の場の方程式
さて、アインシュタインによると、最初にあげた方程式から、彼は多くのややこしい無意味な儀式(まじない)をやっています──彼はハミルトニアン(物理学におけるエネルギーに対応する物理量)を使っています──彼はここでこんなことをやっているのです。そして彼は言います。左側には偏導関数(偏微分係数)があり、これは発散のようなものです。右側は…… この段階では偏微分のことで、発散の話はすぐにします。そして、右側では、ここには物質はなく、重力場にはエネルギーがあるので、エネルギーが必要だ、と言っています。では、彼はどうするのでしょうか?
彼は擬似テンソルというものを作り上げました。──これは上付き文字σと下付き文字μの小さな’t’で、’t’は単に得られる数で、ここにあるように、σとμを等しくすることによって’t’の上付き文字σ 下付き文字μ から得られる不変式なのです。このように。t = t に下付き文字と上付き文字の両方にσをつけると、テンソルを2値分減らすことになります。それで、上付き下付きがないテンソルはスカラー、つまり不変式ということになります。
アインシュタインは擬似テンソルを定義し、これを重力場のエネルギーを記述するのに使います。なぜなら、そこには物質がない、つまり質量がないにもかかわらず、彼はエネルギーを求めるからです。彼によれば、物質とは重力場以外のすべてのものだからです。
アインシュタインにとって重要なことは、重力場以外はすべて物質であるということです。アインシュタインの重力場にはエネルギーがありますから、彼はこれを作り出して(でっち上げて)、それがエネルギーだと言っています。では、どうやって物質源を取り込むのか?
単純に足すのです。エネルギー運動量テンソルを加えます。

混合形式の場の方程式
小文字の’t’に大文字の’T’が加わっているのがわかるでしょう。彼はこの方程式に源(ソース)を加えて拡張し、これが重力場とその源を記述していると言っています。さっきの方程式とは違うように見えますが、同じようなもので、より複雑な形をしています。ここで、大文字の’T’があるのがわかります。これは収縮して得られるものです。テンソルの上付き添え字を下付き添え字にするとき、"縮約"と呼ばれる操作を行います。そして、二次元のテンソル(2値テンソル)の場合、2だけ減るのでスカラーになるわけです。上にひとつ、下にひとつあって、それを打ち消すとスカラーになるわけです。
つまり、エネルギー運動量テンソルと、そこから得られるスカラーを手に入れ、右辺は重力場のエネルギーと運動量、そして重力場の物質的な源であり、エネルギーである、と言っています。そうすると、彼のエネルギー方程式は次のようになります。重力場の全エネルギーは、ソース(発生源)と場そのものです。

保存則
場の全エネルギーと運動量、およびその発生源:
アインシュタインの保存則:
テンソル方程式ではない。
閉じた系では、全エネルギーはこのようになります。
さて、t σμはテンソルではなく、擬似テンソルであることに注意してください。テンソルではないので、テンソルに足すときにテンソル演算はできません。大文字の’T’はテンソルですが、小文字の’t’はテンソルではないので、テンソルの発散はできず、普通の発散をする必要があったのです。つまり、普通の発散を取ると、0になるのです。──彼は、ほら出来上がり!と言っています。これで保存が成立したことになります。
さて、ここでまずいくつかの問題があります。これはテンソル発散ではなく、普通の発散です。理論的に、数学的に保存則を定式化するためには、ゼロにするためにテンソル発散が必要です。しかし、彼はそれができません。その理由をお話ししましょう。

記号サラダ
ワードサラダ
数学サラダ
これを見てください、これからいくつかのシンボル・サラダを見ていきます。一番上はワード・サラダです。"Tuy betnod ve sok voörhedin, onk zor"。
これ、わかりますか?
もしかして、オランダ語?
ダブルダッチ(ちんぷんかんぷん、ナンセンス、理解できない話)かな?
[会場笑]
ご存じですか?
何でもないんです!
どうして?
文のように見え、文のような匂いがし、そこには素敵なヨーロッパ的なものがあります。それで、nought(ゼロ、無)にダブルドットをつけて少し拡大すると、フルストップ(終止符、ピリオド)と大文字とコマ(昏睡状態)があります。言葉のように見えますが、これは戯言です。これはワードサラダですね。
次に、その下にあるものを見てください。ああ!と思うでしょう。これは素晴らしい!と。アインシュタインが書いたものだ、素晴らしい。わかりますか?
これは、その前のものが言葉のサラダであるのと同じように、数学的なサラダなんです。わかるけど、わからないでしょ?
私がそれを証明しましょう。
[会場笑]

ゼロクラスのメトリックス
定理1:ゼロクラスのメトリックス(任意の変数数 n の)は、そのリーマン-クリストッフェル曲率テンソルが等しく消失するという必要十分条件によって特徴づけられる。
注:アインシュタイン宇宙論のリーマン-クリストッフェル曲率テンソルは等しく消滅しない。
ゼロクラスのメトリックス(定量、測定基準)Metrics of zero class は定理です。私が作ったのではありませんよ、数学者に会いに行ってください。いくつもの変数のゼロクラスのメトリックスは、リーマン-クリストッフェル曲率テンソルが等しく消失するという必要十分条件によって特徴づけられます。
さて、アインシュタイン時空のリーマン-クリストッフェル曲率テンソルは等しく消滅しないことに注釈をつけました──だから、この中に入っています。

微分不変量
定理2:クラス0のメトリックスφは非ゼロの微分不変量を持たない。
クラスが0でないメトリックスは、一次の微分不変量を持たない。
1より大きい不変量はφの不変量、リーマン-クリストッフェル曲率テンソル、およびその共変微分である。
帰納的不条理により、t(u)(v)はナンセンスである。
微分不変量──定理2 : クラスゼロのメトリックスφは非ゼロの微分不変量をもたない。非ゼロクラスのメトリックスは一次微分不変量を持たない。1より大きい不変量はφの不変量、リーマン-クリストッフェル曲率テンソルおよびその共変微分(共変導関数)です。ということで、定義、定理1、定理2ができました。
さて、アインシュタインの擬似テンソルを収縮させます。彼はこれをテンソルのように扱っているので、これに対して彼と同じようにテンソル演算を行うと、彼と同じように’t’が得られます。それで、定数’t’あるいは不変量’t’はこのような形をしているのですが、それについてあることに気がつきました。
これは何の関数なのですか?
計量テンソルの成分で、今回は上付き添え字で書かれています。これは別の言い方で、反変テンソルと呼ばれます。上では反変、下では共変、上付きと下付きが混在したテンソルと書くことができます。つまり、それらを入れ替えるだけなのです。δ(デルタ)っていうのはクロネッカーデルタ関数のことで、1か0かのどちらかです。上付き添い字と下付き添い字が同じなら、クロネッカーデルタは1を与え、そうでなければ0を与えます。しかし、ここで、これらのリーマン-クリストッフェル記号、これらのガンマは、前に見たように、計量テンソルの成分とその一次導関数であることも覚えておいてください。
さて、ここでいうアインシュタインの’t’は(不変である)計量テンソルの成分とその一次導関数の関数であり、それ以外のものはないということになります。さて、ここで定理2によって、それらは存在しないことがわかります。そこで、背理法(帰びゅう法)という方法で、アインシュタインの擬似テンソルが数学的に意味を持つと仮定します。これに数学的手続きを適用し、収縮させます。その結果、ガラクタ(ナンセンス)が出来上がる。その前提で何がわかるのか?
ガラクタです!
ということは、彼のエネルギー保存はゴミ(くだらない)だということになります──そんなことはできない──ナンセンスです。全部がナンセンスです!

通常の保存則の破れ
アインシュタインの場の方程式は全エネルギー方程式である
'保存則’である
結論として、アインシュタインの場の方程式はこのような形をとらなければならないのです。もし、物理学のような形をとるのであれば(私はこれを非常に大雑把に使っています)、それは物理学ではありませんが、物理学のような形をとらなければならないからです。つまり、左手にはこの物質があり、それが 'T’です。
ここで、私は混合形式で書いていることに注意してください。
なぜ混合形式で書きたいかというと、テンソルの発散を取るからです。アインシュタインがやったように書きたいので、確認してみてください。──そう、彼はこう書いたのです。
さて、重力場のエネルギーの構成要素の第一項には、宇宙定数(補正係数)もはいっています。そして、あることに気づいてください。──これは重力場のエネルギー運動量と物質源のエネルギー運動量の和なので、エネルギー方程式でもあります。
これはアインシュタインの’E’に小文字の’t’(彼の擬似テンソル)と’T’をつけたものです。さて、それのテンソル発散をとることができるのですが、これが本当に一貫して欲しいことなのです。小さなセミコロンで示したように、テンソルの発散を取ります。共変微分(共変導関数)とテンソル発散をどのように行うかについては心配しませんし、知りたくもありません。私たちが知っているのは、この式のテンソル発散を取るとゼロになる、ということだけです。
ほら、出来上がり!
これで保存則ができました。問題は、何を保存するかということです。というのも、上の方程式を見ると、すべての閉じた系は、この場合(この形のように)全エネルギーが0になります。
これは実験と一致しているのでしょうか?
すべての閉じた系、閉じた系の全エネルギー運動量は常にゼロなのです。これはナンセンスであり、したがって理論全体もナンセンスなのです。このことから、今、締めくくりのコメントに入りますが、ここで少し平静を装ってください。数学で迷っている人たちのために、少し楽しい話をしましょう。私は今、RIGAに来ました。

RIGA: Rusted Iron Gong Award for spectacular phantasmagoria and gross inanity.
壮大なファンタズマゴリア(移り変わる幻影)と総体的な非常識に贈られる錆びた鉄の銅鑼賞。
いいえ、都市 RIGAではありません、錆びた鉄の銅鑼賞 Rusted Iron Gong Award:目を見張るような幻想連鎖と、はなはだしい無意味のためのものです。

そしてノミネートされたのは
1. ヘーラルト・トホーフト、物理学教授、ノーベル賞受賞者、ユトレヒト大学、理由は
「もちろん、まともな天文学者なら、’r’が空間的な距離を表していると主張することはない」
が、しかし。
「……ここで、r₀は中心光源までの光線の最小距離である」
「“普通の"星や惑星は物質を含み、ある半径 r > 2M内で T(sub)μv≠0 となるので、それらについてはシュヴァルツシルト解の有効性はそこで止まってしまう」
ノミネートされたのは、ヘーラルト・トホーフト、物理学教授、ノーベル賞受賞者、ユトレヒト大学、この卓越した至宝です。このことについて彼に話を聞くと、電子メールでこんなことを言っていました。
「私は証拠を持っているので、もし欲しい人がいれば渡すよ。もちろん、まともな天文学者であれば、’r’が空間的な距離を表していると主張することはないだろう」と言うのです。
さて、彼が何と呼んでいたか見たでしょう。彼は五つ持っていましたね?
彼は自分が何を言っているのか分かっていませんでした。──彼は五つ、少なくとも四つ、いや五つあったと思います。でも、一般相対性理論のノートや、ブラックホールのノート(彼自身のホームページ)には、何と書いてあるんですか?
「ここで 'r0' は中心光源までの光線の最小距離」
これって半径じゃないの?
「’普通の’星や惑星は物質を含み、Tµv ≠ 0、……」(そう、物質源)「……特定の半径 r > 2M 以内である、……」(彼の’c’と’g’はひとつで、彼はヒルベルトを使っている)、「……従って、それらにとってシュヴァルツシルト解の妥当性はそこで止まる」
つまり、天文学者や天体物理学者が正しい考えを持っているか間違っているかは別として、トホーフトは、距離であると同時に半径でもあると言っているのですが、まともな人はそんなことしないと言っています。その時、彼は何を吸っていたのでしょう?
ジョス・ブランド-ホーソーンは、私のお気に入りの一人です。この人、シドニー大学のビッグ・クエスチョン研究所の教授なんです。
[会場笑]

そして、ノミネートされたのは
2. ジョス・ブランド-ホーソーン、シドニー大学天体物理学教授、ビッグ・クエスチョン研究所(UNSW)、理由は
「……いくつかの天体は非常に巨大で、脱出速度は基本的に光速であり、したがって光さえも脱出しない」
冗談ではなく、本気で言っているんです。学長は現在、ジョン・ウェッブだと思いますが、彼は私のウェブページを見た人なら誰でも知っているように、私にとっては有名な人です。とにかく、ニューサウスウェールズ大学にはビッグ・クエスチョンのための研究所があります。ブランド-ホーソーンはそこにいますが、彼はシドニー大学と、そこの天文学研究所にもいます。彼はオーストラリアの全国放送でこのように言っています、私はそれを見て、ダウンロードしました
「……いくつかの物体は非常に巨大で、脱出速度は基本的に光速であり、したがって光さえも脱出しない」
そのジャーナリストは、自分が何を言ったのかさえわからず、途方に暮れて座っていましたが、私たちは彼が何を言ったのか知っています。ブラックホールの事象の地平面は、同じ場所に脱出速度があるのとないのとで、分裂病的な性質を持っていると言っているからです。ですから、彼は良い候補者です。
さて、次は昔の仲間、ホーキング博士です。

そして、ノミネートされたのは
3. スティーブン・ホーキング、ケンブリッジ大学物理学教授、理由は
「ビッグバンそのものでは、宇宙の大きさはゼロで、無限に熱かったと考えられている」
しかし
「エネルギーは無から生み出すことはできない」
彼は至る所に姿を現わす、どこにでもいます、"ビッグバン" そのものです。
「ビッグバンでは宇宙の大きさはゼロで無限に熱いと考えられている」
本当に?
大きさもなく、無限に熱い。
では、その温度は何度なんだ、スティーブ?
温度を持つものが必要だと思わないか?
固体なら何だろう?
液体であれば粒子がぶつかり合っているし、気体であれば粒子がぶつかり合っているし、プラズマであれば粒子がぶつかり合っている。粒子がぶつかり合っています。しかし、彼は何も温度を持つことができない、そればかりか、無限であると言っています。
そうなんですか?
無限の温度?
それじゃ意味がない。
何が無限大の温度なんだ?

そして、ノミネートされたのは
4. クレム・プライク、BICEP2科学者、ミネソタ大学物理学者、理由は
「批判されるとしたら、間違っていることよりも、信号を過剰に解釈したことであるべきだ」
クレメント・プライク(クレム・パーキ?)、グーグルの人です。クレメント・プライク、BICEP2の科学者です──BICEP2(主な目的は、宇宙マイクロ波背景放射CMBの非常に弱い偏光を測定すること)を知ってますか?
聞いたことがあると思います。ミネソタ大学の物理学者です。さて、この人たちは、宇宙がまだ…… 宇宙が1兆分の1秒の、1兆分の1秒の、1兆分の1秒しか生きていない時に、いわゆる宇宙マイクロ波背景のBモード偏光をサンプリングした、と言っている人たちです。さて、これはまた妄想の科学です。時計はどこで手に入れたのでしょうか。おそらく、大型ハドロン衝突型加速器を作っているCERN(欧州原子核研究機構)でしょう。
[会場笑]

そして、ノミネートされたのは
5. ラリー・クラウス、アリゾナ州立大学物理学教授、理由は
「……私たちの宇宙は、ほぼ無限にある宇宙の中のたったひとつの宇宙に過ぎないということは、極めて妥当なことのように思われる……」
そして最後の一人は、神の祝福を受けたラリーです。彼はアリゾナ州立大学の教授です。彼は今日、私をてこずらせるためにここに来ていないのが不思議なくらいです。
「……我々の宇宙は、ほとんど無限にある宇宙の中のたったひとつの宇宙に過ぎないというのは、極めてもっともなことのように思われる……」
ラリーはオーストラリアの国営放送でそう言っていました。私はそれを見て、ダウンロードしました。私たちはラリーに聞いてみた。
どこまで近づいたんだ? ラリー、無限数に近づいたの?
あなたは"ほぼ無限数"にたどり着いた。──どこまで近づいたの?
この人たちはどこの学校に行っていたんだろうと思います。前にも言いましたが、私たちはそこに行かなくてよかったと思っています。
[会場笑]

そして、受賞者は
ヘーラルト・トホーフト
ジョス・ブランド-ホーソーン
スティーブン・ホーキング
クレム・プライク
ラリー・クラウス
デッドヒートだ!
それで、勝者は誰でしょうか?
まあ、決められなかったので、デッドヒートです。全員が受賞して、最後に"緑の草と満潮(サザン・ロック・バンド)“になるんです。

緑の草と満潮
ありがとうございました。
──おわり

動画の最後に出てくる「緑の草と満潮」は1960年後半にフロリダで結成されたアウトローズ(無法者、お尋ね者)というグループの楽曲です。スティーブン・クロサーズ氏にとって思い入れのある曲なのだと思われます。
緑の草と満潮
グリーン・グラス・アンド・ハイ・タイズ
ザ・アウトローズ(サザン・ロック・バンド)のトラック10 アウトローズ
グリーン・グラス・アンド・ハイ・タイズ 歌詞
[詩 1:The Outlaws]
いつも夢見る場所で、魂がいつも自由な場所で
銀色のステージ、金色のカーテン、私の頭の中はどこまでも平凡だ
虹が太陽の周りに伸びていくように、僕の上のスターたちはみんな死んでいった
君が見ている景色の向こう側に来たんだ
この素敵な人たちが演奏してくれた
[詩 2:The Outlaws]
今、あなたにこの場所を見せたら、物語はすべて真実となる
本当のあなたを見るために あなたの顔を通過させてくれる?
それは私のためではない私が王であるかのようにこの質問をする
愛し、信じ、感じなければならないから
タンバリンのはじける音に誘われる前に
[コーラス:The Outlaws]
緑の草原と満潮は永遠に
石の城、魂と栄光
失われた顔は、僕たちがあなたを崇拝していると言う
王と女王があなたのためにお辞儀をして演奏するように
[Guitar Solo]
[詩 3:The Outlaws]
僕を信じない人は、自分の魂を見つけて自由にしてくれ
信じてくれる人は、時間が鍵になることを知り、信じてくれ
何度も何度も心の安らぎを与えてくれた彼らに感謝している
音楽と韻の中で自分を見つける手助けをしてくれた
そこであなたを魅了する
[コーラス:The Outlaws]
緑の草原と満潮は永遠に
石の城、魂と栄光
失われた顔、私たちはあなたを崇拝していると言う
王と女王があなたのためにお辞儀をして演奏するように
[エンディング]
Yeah, play for you
[Guitar Solo]
アウトローのヘンリー・ポールはこう語っている。
「……ローリング・ストーンズのベスト盤で『High Tides and Green Grass』というアルバムが出ていた。それはローリング・ストーンズのベスト盤の名前だった。これは1966年のことだよ。で、そのタイトルを逆にしたのが、"Green Grass and High Tides"という表明だったんだと思う。それくらいは知ってるよ。
ジャニス・ジョプリンからジミ・ヘンドリックスまで、ロックンロールの輝ける人たちのために書かれた曲で、マリファナとは何の関係もないことも知っている。でも、ある特定の人物の歌詞にある……「王と女王があなたのためにお辞儀をして演奏するように」ということと関係があると思うんだ。ジミ・ヘンドリックスとジャニス・ジョプリンのことだ。"石の城、魂と栄光"
この曲の多くは、何の関係もない言葉をコラージュしたもので、ただフィットして響きが良かっただけだ。でも、僕の好きな歌詞のひとつだ。僕の曲作りはスタインベック的で、正確さと現実に根ざしたものだけど、これは間違いなく『不思議の国のアリス』だね。
Baking a Cake 1
All Black Hole universes All Big Bang universes
⑴ Spatially infinite, Spatially (k=1), or spatially infinite (k=-1, k=0)
⑵ Eternal, Finite age (~13.8 billionyr)
⑶ Contain only one mass, Contain many masses and radiation
⑷ Not expanding (static, stationary), Expanding (non-static)
⑸ Asymptotically flat (or asymptotically curved), Not asymptotically anything
⑹ No k-curvature, k-curvature
Holes and Bangs are mutually exclusive by definition.
Baking a Cake 2
.1. Black holes are schizophrenic – they have and do not have an escape velocity simultaneously at the same place (at the 'event horizon’).
. 2. The finite black hole mass produces infinite gravity!
.3. X = black hole universe, Y = big bang universe
Black hole and big bang universes are figments of irrational imagination.
Baking a Cake 3
Every 'black hole’ encounters infinite gravity at each and every other 'black hole’.
None of these holes are asymptotically anything! Contra-hype!
Baking a Cake 4.1
Einstein tensor, Ricci tensor, Ricci scalar, metric tensor, Energy-momentum tensor, λ is the 'cosmological constant’.
Baking a Cake 4.2
Material sources are both present and absent by the same mathematical constraint, T(uv) =0!
Numerology 101
The 'Schwarzschild solution’ : Hilbert’s magic trick!
From this the black hole was Stillborn.
Insinuation of Newton
The 'Schwarzschild radius’ is,
Hence, Escape speed!
Cosmologists in Confusion
Hilbert’s 'r’ is,
⑴ The areal radius;
⑵ The coordinate radius;
⑶ The radius; (e.g. Gerardus 't Hooft, Nobel Laureate)
⑷ The distance; (e.g. Gerardus 't Hooft, Nobel Laureate)
⑸ The radial coordinate; (e.g. Gerardus 't Hooft, Nobel Laureate)
⑹ The radius of a 2-sphere;
⑺ The reduced circumference;
⑻ The radial space coordinate;
⑼ A gauge choice; it defines the coordinate r. (Gerardus 't Hooft, Nobel Laureate)
Surface Theory
The First Fundamental Quadratic Form
Metric Tensor as a Matrix
The metric tensor for a surface
The determinate of the metric tensor for a surface
Gaussian Curvature
The intrinsic geometry of a surface is entirely independent of any embedding space. The surface in Hilbert’s metric is,
Its Gaussian curvature K is calculated by,
The Real Identity of Hilbert’s 'r’
So the Gaussian curvature is,
The radius in Hilbert’s metric
Minkowski’s Metric (SR)
The radius is,
The gaussian curvature is,
Schwarzschild’s solution
Hilbert’s solution is not equivalent to Schwarzschild’s.
Solutions of Droste and Brillouin
Droste’s solution
Brillouin’s solution
The Schwarzschild’s ground-form
An infinite set of equivalent solutions.
Setting Equivalent Solutions
Can Droste’s solution be extended to 0≤r to produce Hilbert’s solution (and hence a black hole)?
No, it can’t!
Metric Extensions?
Thus, none can be 'extended’.
The black hole does not exist.
Gaussian curvature Invariant
This is a positive finite invariant.
The Kretschmann scalar
In the case of Schwarzschild form it is,
This is always finite, and invariant.
The Acceleration Invariant
The radial geodesic acceleration of a 'point’ in Schwarzschild spacetime is given by,
This is an invariant condition.
Kruskal-Szkeres 'coordinates’
This does not extend to R(c)=0.
Once again, the black hole is a fairy tale.
Generalisations
Schwarzschild’s 'black hole’: – charge neutral, no rotation.
The Reissner-Nordström 'black hole’: – charged, no rotation.
Kerr 'black hole’: – charge neutral and rotates.
Kerr-Newman 'black hole’: – charged and rotates.
What is the overall ground-form?
The Overall Metric Ground-Form
The infinite set of equivalent solutions is given by,
None are Inextendible
r² can’t take negative values. The black hole is a fallacy.
The Overall Gaussian Curvature
This is not spherically symmetric, but reduces thereto.
The Overall Kretschmann Scalar
This is always finite.
Isotropic Schwarzschild Ground-Form
Isotropic Schwarzschild Radius
There is no 'black hole’.
Isotropic Schwarzschild Gaussian Curvature
The invariant is:
There is no 'black hole’.
Acceleration Invariant for the Isotropic Schwarzschild Form
Therefore there is no black hole!
Riemannian Curvature
Generalises Gaussian curvature to dimensions > 2.
Isotropic Point
Definition: If the Riemannian curvature at any point is independent of direction vectors at that point then that point is called an isotropic point.
Riemannian Curvature of Schwarzschild spacetime
Riemannian Curvature: the Schwarzschild Invariant
r₀ yields an isotropic point.
Riemannian Curvature of Isotropic Schwarzschild Spacetime
Riemannian Curvature: the Isotropic Schwarzschild Invariant
All the Calculations
Crothers, S. J., General Relativity: In Acknowledgement of Professor Gerardus 't Hooft, Nobel Laureate, https://vixra.org/pdf/1409.0072v6.pdf
Field equations in the Absence of Matter in Another Form
Field equations in the Absence of Matter in Mixed Form
Field equations in Mixed Form
Conservation Laws
Total energy and momentum of field and its sources:
Einstein’s conservation law:
Not tensor equations.
Symbol Salads
Word Salad
Tuy betnod ve sok voörhedin, onk zor
Mathematics Salad
Tuy betnod ve sok voörhedin, onk zor
Metrics of Zero Class
Theorem 1: Metrics of zero class (of any number of variables n) are characterized by the necessary and sufficient condition that their Riemann-Christoffel curvature tensor vanishes identically.
Note: The Riemann-Christoffel curvature tensor for Einstein’s spacetimes does not vanish identically.
Differential Invariants
Theorum 2: Metrics φ of class zero have no non-zero differential invariants.
Metrics of non-zero class have no first order differential invariants.
The invariants greater than one are the invariants of φ, the Riemann-Christoffel curvature tensor, and it’s covariant derivatives.
By reductio ad absurdum, t(u)(v) is nonsense.
Violation of the Usual Conservation Laws
Einstein’s Field Equations are total energy equations
The 'Conservation Law’
RIGA
Rusted Iron Gong Award for spectacular phantasmagoria and gross inanity.
And the Nominees are:
1. Gerardus 't Hooft, professor of physics, Nobel laureate, Utrecht University, for
“Of course, no astronomer in his right mind would claim that 'r’ stands for a spatial distance."
BUT,
“…where r₀ is the smallest distance of the light ray to the central source."
“'Ordinary’ stars and planets contain matter, T(sub)µv ≠ 0 within a certain radius r > 2M, so that for them the validity of the Schwarzschild solution stops there."
And the Nominees are
2. Joss Bland-Hawthorn, Professor of Astrophysics, Sydney University, and the Institute for Big Questions (UNSW), for
“…some objects are so massive that the escape speed is basically the speed of light and therefore not even light escapes."
And the Nominees are
3. Stephen Hawking, Professor of Physics, Cambridge University, for
“At the Big Bang itself, the universe is thought to have zero size, and to have been infinitely hot."
BUT
“energy cannot be created out of nothing"
And the Nominees are
4. Clem Pryke, BICEP2 Scientist, Physicist, University of Minnesota, for
“If we are to be criticized, it should be for over-interpreting the signal, rather than for being wrong."
And the Nominees are
5. Larry Krauss, Professor of Physics, Arizona State University, for
“…it seems quite plausible that our universe may be just one universe in what could be almost an infinite number of universes…"
And the Winners are
Gerardus 't Hooft
Joss Bland-Hawthorn
Stephen Hawking
Clem Pryke
Larry Krauss
It’s a dead heat!
最後までお読みいただき、ありがとうございました。



![自己組織化プラズマがビルケランド電流を形成 - NASA ; Jaybear 編集, Public domain, via Wikimedia Commons [44].](https://quietsphere.info/wp-content/uploads/9.150px.png)