電気的宇宙の幾何学②──幾何学模様を駆動しているエネルギーは何なのか?
- 1. 磁気流体力学の10パターン
- 1.1. バディ・ジェームズ:磁気流体力学
Buddy James: Magnetohydrodynamics- 1.1.1. ① 音響浮遊の水滴 Water Droplet in Acoustic Levitation
- 1.1.2. ② ヘリコン波 Helicon Waves
- 1.1.3. ③ ビルケランド電流 Birkeland Currents
- 1.1.4. ④ 土星の北極 North Pole of Saturn
- 1.1.5. ⑤ 雷の内部構造 Interior Structure of Lightning
- 1.1.6. ⑥ セオドーティアン・ルーツ Theodoughertian roots
- 1.1.7. ⑦ 渦、キラリティ、キャビテーション Vortices, Chirality and Cavitation
- 1.1.8. ⑧ 青い渦(旋回)The Blue Whirl
- 1.1.9. ⑨ キンク不安定性 Kink Instability
- 1.1.10. ⑩ リヒテンベルク図形 Lichtenberg Figures
- 1.2. クリスタル・スパイラルとセオドーティアン・ルーツ
- 1.3. 共有:
- 1.1. バディ・ジェームズ:磁気流体力学
磁気流体力学の10パターン
バディ・ジェームズ氏は今回紹介する動画の結語として「ドハティセットとEU(Electric Universe)モデル自体が、磁気流体力学の複雑な動的幾何学をミクロからマクロまで、あらゆるスケールで理解するための枠組みを提供してくれることが明らかになった」と言います。とはいうものの難解過ぎて、わからないことだらけです。
前回の記事でも多くの複雑で美しい図形が登場しました。一見、複雑に見える図形も単純な図形が回転し、重なり合い、立体的に螺旋状に組み合わさっているだけだと捉えることもできます。その意味では、前書きにある動画の[要旨]の中に記された「ウォル・ソーンヒルからのメモ」は、この「驚くべき複雑さ」を簡潔にまとめているように思います。これらの幾何学模様を駆動しているエネルギーは何なのか。ビルケランド電流が、それを解く大きな鍵であることは間違いないと思いますが、また、そこからできた幾何学模様がどのようなエネルギーを生み出すのか? なぜそうなるのか? 興味は尽きません。
2017年、バディ・ジェームズが発表した「青い渦の対向螺旋渦の分類が、六つの対向螺旋渦の集合で構成されていることを紹介する論文」を紹介します。

(以下、引用)
ドハティセットは高次元空間の葉状構造(縞状構造)を表しているが、それはまた他のものと同様に内部空間でもある。TDS(ドハティセット)は射影力学幾何学であり、螺旋とトロイダル/ボルテックスに基づくフラクタルプラズマ物理学である。逆二乗とヘテロダイナミック位相共役を用いた爆縮・爆裂するファイ・スケーリングにより、TDSは対数的なスケール不変性を持つ。電気工学、ホモトピー型理論、統合情報理論、ひとつの要素を持つ分野、グラフェン、その他多数の相互に関連する分野で有望である。誘電体慣性面は、キス球から絞り出される。
連続するイメージは、科学と数学の分野の異常から私自身が開発した幾何学であるドハティセットに固有のものである。

青い渦──対立する渦巻きの分類法。91 x 60 cm、色鉛筆・インク
これは、昨年メリーランド大学で発見された"青い渦"の形状に類似していると私は考えている。ここに見える青い渦は、再帰的、ヘテロダイイング、入れ子、対向螺旋渦OSVで、層状コヒーレンスを形成している。TDSは、情報の足場として、最初の反復がフィードバックループとなるコボルディズムとして有望視されている。これは、渦をベースにした流体力学の研究を促進し、フラクタルラティスにおける球体積層の起源となる数学の言語でもある。祖父(OSV)は外側のモードで見られ、内部には二つの親 OSVがあり、それぞれの親 OSVは孫 OSVを持ち、全部で六つの OSVフォリエーションを構成している。ファイ・エアロ/フルイド・ダイナミクス。

TDS──電気的プラズマ宇宙 91 x 60 cm 紙に色鉛筆、インク
左の青は、ドナルド・E・スコット博士の「ビルケランド電流のベッセル関数モデルは、これらの電流が中空同心円状の二重回転円筒形電流シートで構成されていることを明記している」という表現が最も適切かもしれない。ビルケランド電流は、惑星のオーロラであり、グローモードのプラズマのシートである。私は、原子的にはすべての物質がこれと同じ演算子を使っていると提案する。TDSは全てを網羅するトロイダル磁場であり、トロイダル磁場の中にトロイダル磁場を拡張する指数磁場である。写真の右側で赤くハイライトされているカドゥケウスは、内側にも外側にも投影的に拡大することができる。現実の螺旋状の性質は、驚くほど単純で、調和的な直感的なものである。波動力学は多くの余地を露出させる。次元は爆縮/爆裂する誘電体である。

[要旨]
磁気流体力学は、磁場の存在下で導電性流体の挙動を研究する物理学の一分野である。磁性流体の例として、プラズマ、液体金属、塩水、電解質などがある。ドハティセットの予測解析とそれが電気的宇宙モデルにどのように適用されるかを理解するために、学際的な幾何学者のバディ・ジェームズは、磁気流体力学の電流、流れ、パターンに関する10の実世界での検証を図解している。
──ウォル・ソーンヒルからのメモ
数学的な理論が本当の意味を持つのはそのときだけである。しかし、我々は常に数学とモデルとの関連に注意しなければならない。"プラズマ宇宙論の父"であるハンス・アルヴェーンは、1970年のノーベル賞受賞スピーチで、彼の磁気流体力学(MHD)理論が宇宙プラズマに適用されれば、危機的状況になると警告した。この間違った理論モデルのために、宇宙物理学者は電気的な宇宙に対して盲目になってしまった。彼らは頻繁に新しい発見に驚き、魔法のように発生する磁場を発明することを余儀なくされている。しかし、バディ・ジェームズは、ドナルド・E・スコットの電気的なビルケランド電流構造に関する素晴らしい研究を紹介し、実際の物理モデルから生じる驚くべき複雑さを示している。
バディ・ジェームズ:磁気流体力学
Buddy James: Magnetohydrodynamics

ドハティセットの予測解析と、それが電気的宇宙モデルにどのように適用されるかをより理解するために、磁気流体力学の電流、流れ、パターンに関する10の実世界での応用と事例を紹介することにしましょう。しかし、その前に、ドハティセットとはいったい何なのか、その理解を単純化することにします。
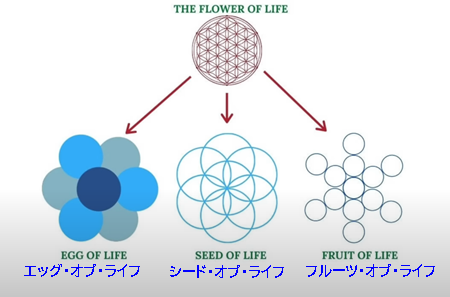
このセットは、シンプルに多くの人がすでに知っている"フルーツ・オブ・ライフ"と"フラワー・オブ・ライフ"の配列のその次の繰り返しです。フラワー・オブ・ライフは、世界中の寺院や神聖な場所で見られる古代のモチーフです。

この概念は非常に重要ですが、もう一歩進めて、ここにあるフルーツ・オブ・ライフを、逆二乗ベッセル関数をパラメータとして、一層、また一層と回転させると、ドハティセットが構成されます。
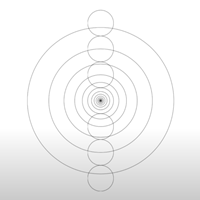
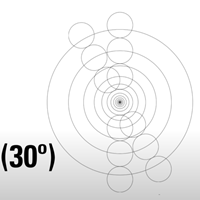


これについては、この後、セオドーティアン・ルーツ Theodoughertian roots を探るときに詳しく説明します。これがドハティセット(集合)の組み立て方です。
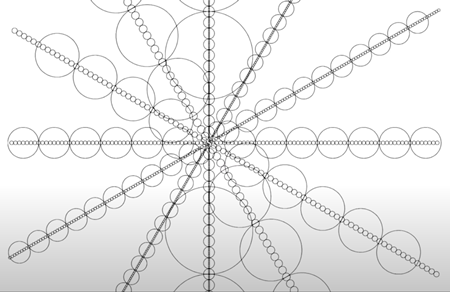
ドン・スコットが最新のビデオで雄弁に語ったように、すべては 1/r です。
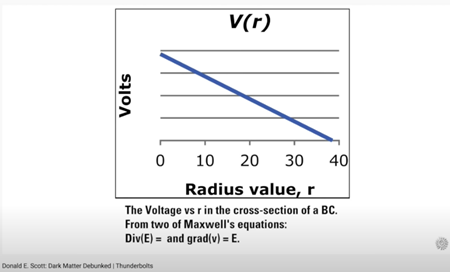
BCの断面における電圧対r。マクスウェルの方程式の二つから :
おそらく、この幾何学は、ドン・スコット教授が同様に仮説を立てたビルケランド電流のように、回転とスピンの起源を提供します。
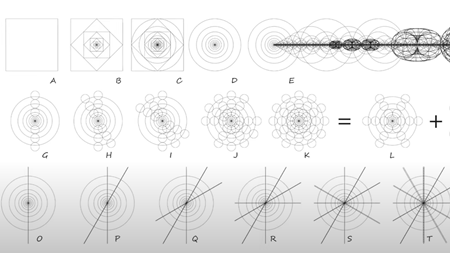
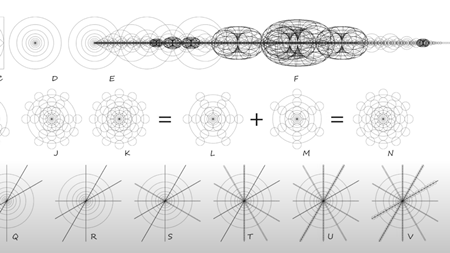
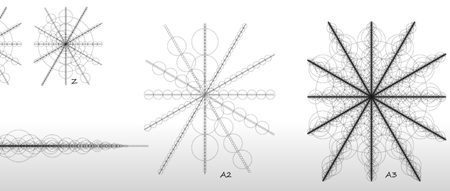
確かに、この創発(部分の性質の単純な総和にとどまらない性質が、全体として現れること)の動的幾何学が、ビルケランド電流の構築の基本であることは理にかなっています。この表現は磁気流体力学の流れに関するものなので、磁気流体力学とは何かということを定義しておきましょう。

磁気流体力学とは、磁場が存在するときの導電性流体の流れを研究する学問です。プラズマを完全な導電性流体として扱うモデルは、磁化されたプラズマの平衡と大規模安定性の特性を記述するための最も成功したモデルです。

このような磁性流体の例としては、プラズマ、液体金属、塩水、電解質などが挙げられます。

① 音響浮遊の水滴 Water Droplet in Acoustic Levitation
これらの流れについては、他のエピソードで詳しく説明する予定ですが、とりあえずは音響浮遊のシンプルな水滴から始めます。(※水滴が宙に浮く)


第二高調波

第三高調波

第四高調波
周波数が高くなるにつれて、それぞれの高調波がドハティセットの枠組みの中でどのように入れ子になって収まっているかざっと見てみましょう。




これらの形は自然な3Dサイマティクス(砂や水などの媒質によって物体の固有振動や音を可視化すること、またはその現象の研究)です。
② ヘリコン波 Helicon Waves
さて、これらの図形がトンネルの中を移動しているところを想像してみましょう。ただのトンネルではなく、遍在する電気回路に直接接続された空間のトンネルです。
このプラズマチューブ、つまり電流は実際に存在し、ヘリコン波 helicon waves と呼ばれています。
※ヘリコン波:磁場を加えた固体プラズマの中を伝わる電磁波の一種。 1960年 P.アイグラインにより存在が理論的に予言された。磁場のないプラズマでは,プラズマ振動数よりも低い振動数の電磁波は減衰して,プラズマ中を伝わることができない。しかし,磁場が存在するとプラズマ振動数よりも低い振動数の電磁波も伝わることができる。磁場に平行に進行して,波の振動電場成分が螺旋運動をする。真空中の光や空気中の音は振動数によらず一定の速さで伝わるが,ヘリコン波は振動数が高いほど速く伝わる性質がある。電離層中を地磁気に沿って伝搬する電磁波をホイスラー波と呼んでいるが,これに相当した波を固体プラズマではヘリコン波という。ギリシャ語「曲がりくねった(山)」の意
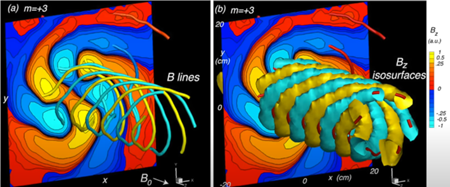
波動は存在し、しばしば電流や流れの構造全体の幾何学的形状を構成しています。ヘリコン波は、私たちがオーロラとして見ているものであり、そう、音もするのです。文字通り天の音。
オーロラを見るときは、それが文字通り3Dサイマティクス(音と振動の目に見える効果に関する研究)であることを知っておいてください。そして、次のタイプの電流であるビルケランド電流にたどり着きます。
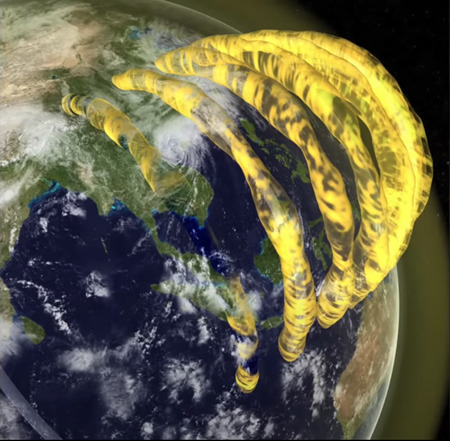
③ ビルケランド電流 Birkeland Currents

ガウス型ベッセル・フィラメントやビルケランド・フィラメントには、複雑な幾何学模様が存在します。
※ベッセル関数とは
ベッセル関数は、その関数を詳細に研究したベッセルという人(F. W. Bessel 1786-1846)にちなんで名づけられた関数です(1824年)。ベッセルはドイツの天文学者で惑星の動きの研究の過程でベッセルの微分方程式及びその解のベッセル関数を得たそうです。ちなみにベッセルの天文学者としての最初の顕著な業績は、ハレー彗星(Halley’s comet)の軌道を計算したことだそう。
ベッセルの微分方程式及びその解であるベッセル関数は、自然界の様々な物理現象のモデリングの際に登場します。一見全然関係ない現象がどれもベッセルの部分方程式で記述されて、ベッセル関数に従う挙動を示すというのはとても面白いものだと思います。
※ガウス関数とは釣鐘型を示す関数
④ 土星の北極 North Pole of Saturn
例えば、土星の北極を見てください。
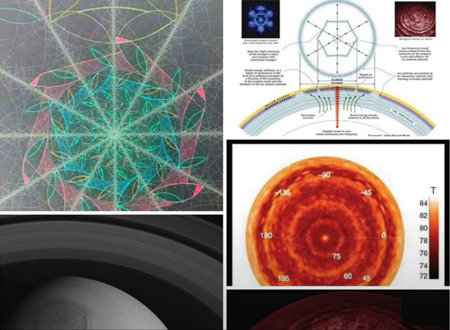
この六角形の幾何学模様は、電気的な太陽から来るビルケランド電流によって作られ、また、持続しています。逆回転をする花びらに至るまで、その類似性を見てみましょう。

では、地球に話を戻して、稲妻の幾何学についてお話ししましょう。ここで、ビルケランド電流を示す波の中に波が入り込んだような挙動は、電荷を効率的に分配するための基本的な形状を持ち、このカドゥケウス caduceus-like のような編み込みは稲妻のフィラメントの中まで続いているはずで、実際にそうなっています。
※カドゥケウス:ギリシア神話のヘルメース神の携える杖。しばしば"杖にからむ蛇"として表される螺旋は生命力や権威などを象徴している。本来のカドゥケウスは、先端から伸びた二本の小枝が本体に絡む木の枝であり、水脈を探す"占い棒"に近かったと見られる。後に、小枝は蛇の形へと変わった。(ウィキより)
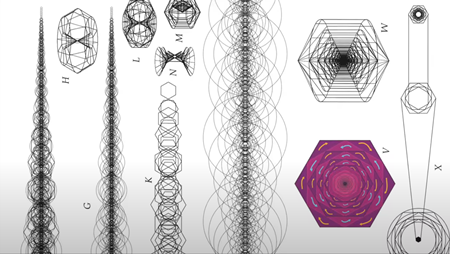
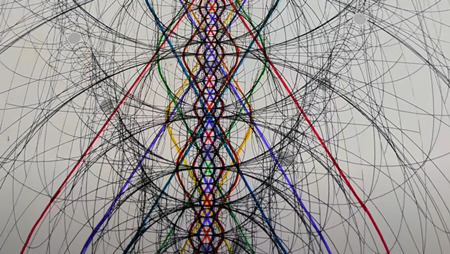
⑤ 雷の内部構造 Interior Structure of Lightning
ウェイン・バーン Wayne Burn が書いた「放電による多角形クレーターの形成※」という論文では、電荷が六角形のチューブ、またはシース(鞘)を形成し、各層が逆回転しながら稲妻の中を流れていることを示しています。
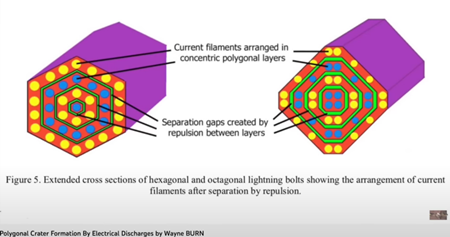
※「グローバルテクトニクスの新概念」というPDFファイルの p.15に「放電による多角形クレーターの形成」(ウェイン・バーン)の論文が日本語に訳されています。https://www.ncgtj.org/NewsLetterJ/NCGTJ3-2J.pdf
これは、これまでお話ししてきた他の流れと似ています。
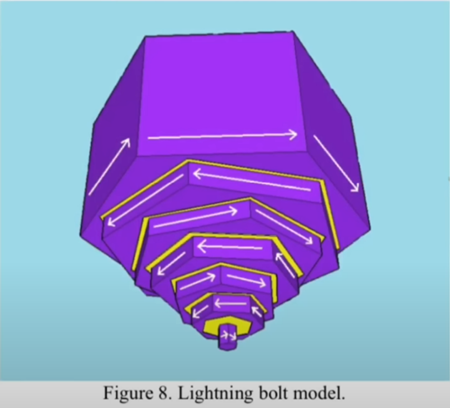
このような形状の多角形クレーターの証拠は、月も含め、惑星の至る所で見つけることができます。


このプロセスは、"電気的傷付処理 electrical scarification“とも呼ばれています。この電荷と電荷の分離の幾何学的過程をさらに証明するのが、セオドーティアン・ルーツです。
⑥ セオドーティアン・ルーツ Theodoughertian roots
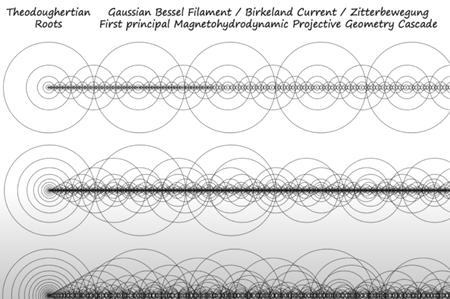
ガウスベッセルフィラメント/ビルケランド電流/ツィッターベヴェーグンク/第一原理磁気流体力学 射影幾何学カスケード
セオドーティアン Theodoughertian roots(theodorianテオドリアン?)・ルーツは非常にわかりやすく、水滴と同じように、ハーモニクス(高調波)とともに段階的に、辺の〈数〉を増やしていきます。まず、電荷の中性は、先ほど稲妻で見たように、エッジを探し求めます。それを知った上で、まず多角形を使います。それから、多角形同士を均等に入れ子にして、逆三角形、逆四角形、逆六角形などの幾何学的な形状得ることができます。
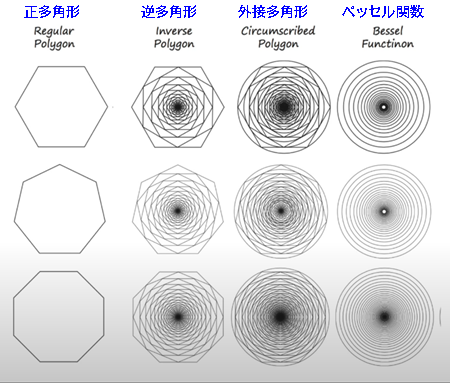
次に、多角形を束ねる、つまり外接させると、ベッセル関数が得られます。このベッセル関数は、私たちの指紋や原子の特異性と同じように、ひとつひとつがユニークです。そこから、最初のベッセル関数から外側へカスケード的にベッセル関数を繰り返していきます。
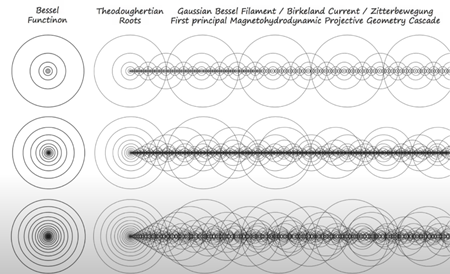

この射影幾何学的な構成が、フィラメントを形成しています。これがドハティセットとビルケランド電流形成の第一原理幾何学の構築方法です。すべてキャビテーティング(空洞形成)です。
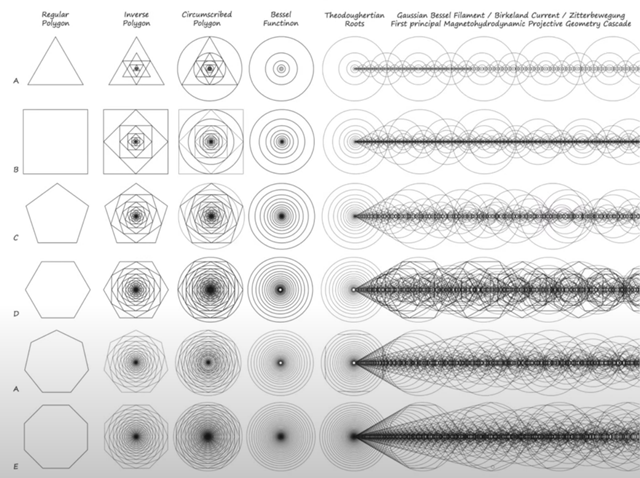
このフィラメントに沿って、建設的および破壊的な波の干渉も起こり、これが私たちが経験する現実に大きく関わっています。

破壊的干渉とは、同じ方向に進む二つの波が、一方の波の頂上と他方の波の谷間で一直線に並ぶことです。波が打ち消されます。
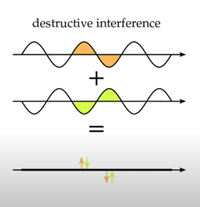
建設的干渉とは、同じ方向に進む二つの波が重なり、その波頭が結合してより大きな波が発生することです。
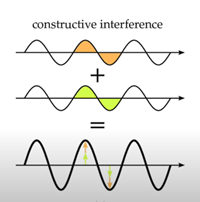
次の流れは、渦、キラリティー chirality、キャビテーション cavitationです。
※キラリティーとは、三次元の図形や物体や現象が、その鏡像と重ね合わすことができない性質のこと。キラリティがあることをキラルという。カイラリティ、カイラルともいう。これらの語はギリシャ語で"手"を意味するχειρ (cheir) が語源である。手はキラルなものの一例で、右手とその鏡像である左手は互いに重ね合わせられない(右手の掌と左手の甲を向かい合わせたときに重なり合わないということである)。
⑦ 渦、キラリティ、キャビテーション Vortices, Chirality and Cavitation


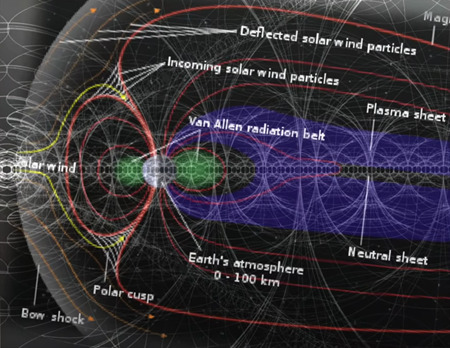
まず、極うずと磁気圏を観察します。
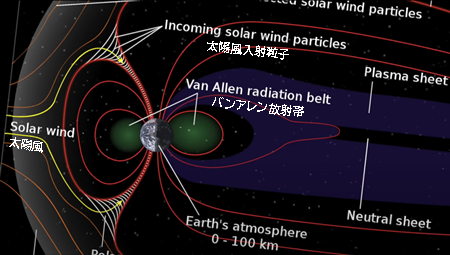
次に、ドハティセットの"渦のテクスチャー vortexture“を重ねて観察してみましょう。
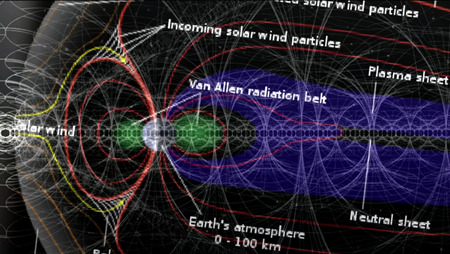
文字通り、"渦のオーケストラ
vorchestra“のようなものです。
この"渦のオーケストラ"は、体のあらゆる部分を取り囲む筋膜、つまり筋状の結合組織の鞘(シース)のようなものと考えることができます。
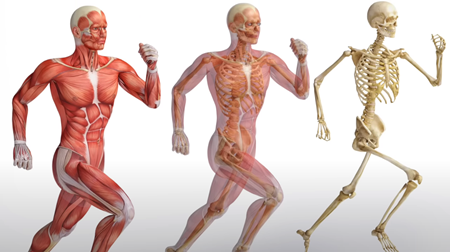
それは電気的なもので、私たちの身体を通して、この器官全体に沿って、すべての思考を光の速さで動かしています。
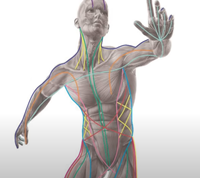
しかし、この"渦のオーケストラ"はあらゆるスケールにあり、宇宙のすべてをつないでいます。
これを別の言葉で言うと、"宇宙コネクトーム(神経回路マップ)“とも言います。電磁場が形をつくり、形が力をもっていることがわかります。


渦が時計回りや反時計回りに回転するキラリティも電磁気の力のひとつで、しばしばコリオリ効果によって制御されています。
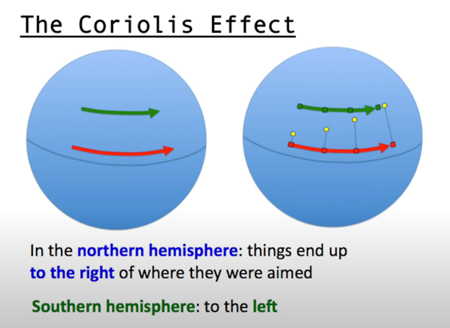
北半球では物事は狙ったところよりも右側に寄ってしまう。南半球は右へ
このような渦は、銀河系からマイクロ・スパイア(spire:尖塔、らせん、渦)のキャビテーションまで、あらゆるスケールで形成されています。
次の例では、これまでに紹介した流れをいくつか組み合わせてみます。

⑧ 青い渦(旋回)The Blue Whirl
2016年、研究者たちは新しいタイプの火、青い渦(旋回)blue whirls を発見しました。
青い渦は、混沌とした火の渦から発展し、ほぼ煤の出ない燃焼をする渦巻き状の火炎現象です。

スーパーコンピューターによるシミュレーションで、青い渦の炎の構造や流れの構造が明らかになりました。
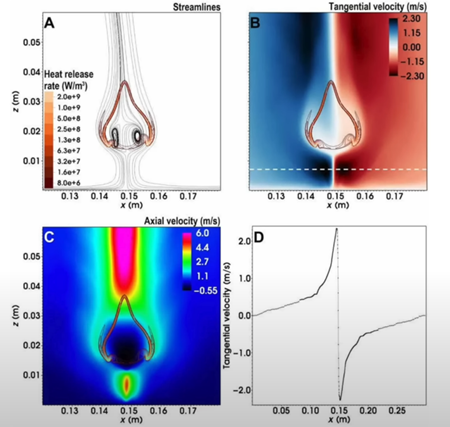
この時点で、私はすでに何年も前からこの形をスケッチしており、大局的な意味での重要性を知っていました。

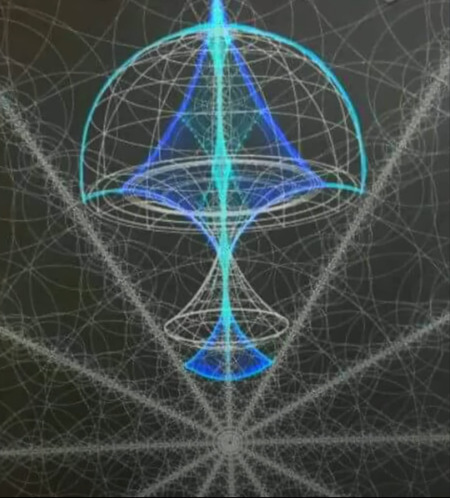
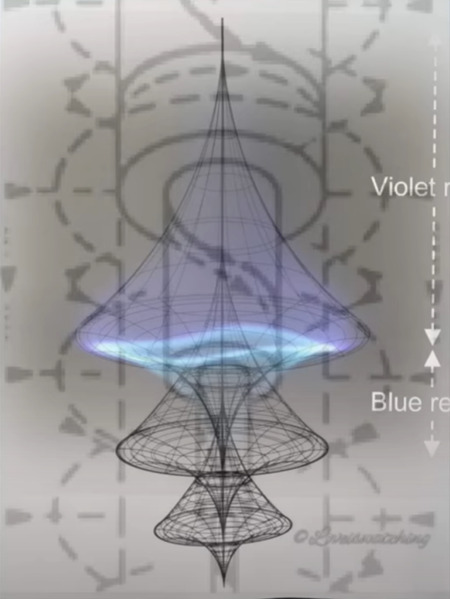
それで2017年、私は青い渦の対向螺旋渦の分類が、六つの対向螺旋渦の集合で構成されていることを紹介する論文を発表しました。(前書きで紹介した論文)
2019年には、コーネル大学が発表した論文で、"青い渦"の渦巻きは三種類の炎で構成されていることがわかりました。
そうして、集合(セット)の予測力がなんとなくわかってきたのです。

予測といえば、この幾何学は、ビルケランド電流の底面、あるいはビルケランド電流が極に入れ子になって積み重なる様子が、青い渦の形に似ていることを予測しています。
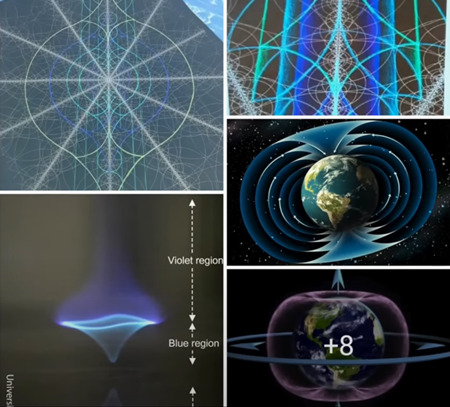

このヘテロダイン heterodyning、位相共役の積み重ね phase-conjugate stacking で思い出したことがあります。

位相共役 Phase conjugation は、黄金比の倍数です。


驚くことに、この形状が現れるもう一つの流れは、イーロン・マスクのスペースXラプターエンジンの実験にあります。
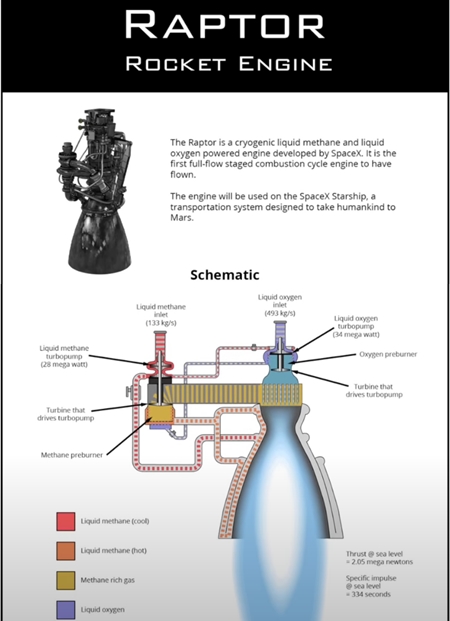
この特殊な形状は、最小限のエネルギー構成を示し、また、レンズフレアにも顕著に現れています。

⑨ キンク不安定性 Kink Instability
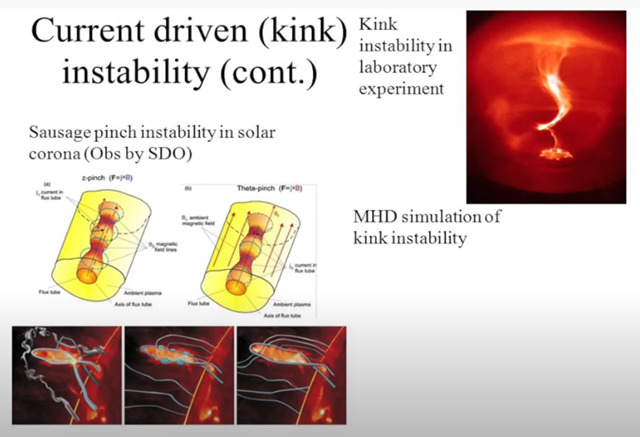
キンク不安定性 kink instability は電流駆動型のプラズマ不安定性で、プラズマ柱の断面が質量中心から横方向に変位することを特徴とし、プラズマの特性には変化がありません。
つまり、基本的には、このドハティセットに見られるようなカドゥケウス(杖にからむ蛇)の編み込みと極めて似ています。これが最初の10個のコンカチネーション concatenation(鎖状に連結すること、出来事などの連続、連鎖)です。

コンカチネーション(連結)とは、相互に関連した一連の物事や出来事のことです。一般に、あらゆるスケールで大小さまざまなキンク kink(ねじれ、よじれ)の不安定性がペアリングや入れ子になっており、その数は未知数です。
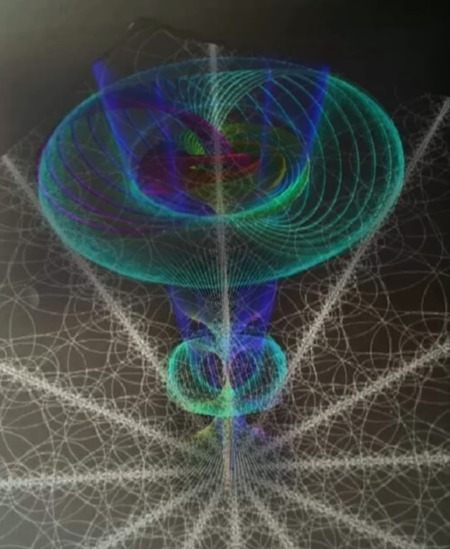
無限に続くトロイダル・ノード(ドーナツ形の結節点)、ヘリカル(らせん状)、同軸コイルのマッピングには、まだ多くの研究が必要です。

ここで強調しておきたいのは、トロイダル・ノードという言葉です。というのも、らせん状のフィラメントの中心には入れ子状になった"トーラス tori (torusの複数形)“があり、これらの入れ子状の"トーラス tori “は、あらゆる恒星が放つ宇宙のベッセル関数の繰り返しでもあるからです。
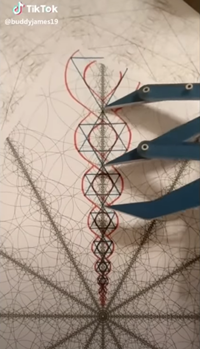
⑩ リヒテンベルク図形 Lichtenberg Figures
この最後の例では、枝分かれシステム、つまり根の木 roots trees、宇宙の物質分布、リヒテンベルク・フロー(流れ)、あるいは樹枝状の樹枝状分岐 arborization があります。




いろいろな呼び名があります。この形状は、宇宙中の多くの生物で起こっています。すべてが電気的であることを思い出させてくれる形状のひとつです。私たちのシナプスの脳活動、静脈、臓器、そして暗黒物質という仮説さえも、実はビルケランド多相ウェブ Birkeland polyphase web なのです。
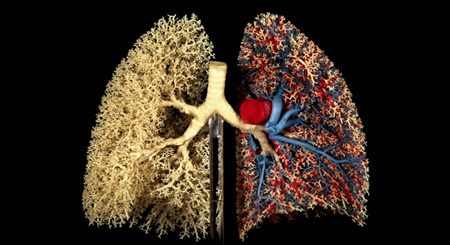
自然界には、このように美しい形をしたものがたくさんあります。


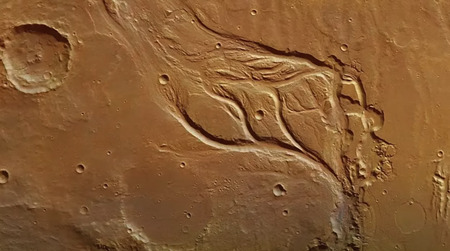
リヒテンベルク・フローは、しばしば生命システムの兆候であったり、かつて生命システムがそこにあったことの痕跡であったりします。このように全体として、宇宙論は魅力的で、多種多様な流れでいっぱいです。そしてまた、ドハティセットとEU(Electric Universe)モデル自体が、磁気流体力学の複雑な動的幾何学をミクロからマクロまで、あらゆるスケールで理解するための枠組みを提供してくれることが明らかになったのです。


──おわり
クリスタル・スパイラルとセオドーティアン・ルーツ
この動画では、バディ・ジェームズがジョージ・レオニアクと、フラワー・オブ・ライフ、シード・オブ・ライフ、チャクラ、神聖幾何学などについて話しています。
#55 George Leoniak- Implosive & Explosive Knew Geometry, Krystal Spiral & Theodoughertian Roots
今日は特別に、YoutubeチャンネルKnew Geometryのジョージ・レオニアクさんをお招きしています。このような、私たちのコンテンツがどのように収束していくのか、また、私たちの発見がどのような意味を持つのか、情熱的な会話と考察にご期待ください。ジョージさんのYoutubeチャンネルKnew Geometryへのリンクはこちらです。
https://www.youtube.com/c/KnewGeometry。
今年もたくさんのイベントが開催されます。
北米2022年プラズマ電磁気宇宙会議の正式な日付と会場は、2022年8月14日(日曜日)になるそうです。2:00pm- 2:00am at 715 E Milwaukee Ave, Detroit, MI 48202 The Tangent Gallery
もしあなたが会議でパフォーマンス、ベンダー、ボランティア、スピーチをしたいのなら spectrumcontracting23@gmail.com に直接メールを下さい。……CALL FOR VENDORS, SPEAKERS, PRESENTERS AND PERFORMERS!!!!!!!
ぜひご登録ください。また、あなたがそうする必要性を感じるなら、コメントや質問をしてください。あなたの思考に興味を持っていました。
「すべての構造には形があり、TDN(The Doherty Network)は力の図として形を提供し、実際、すべての基本的な力はシンプレックスを使用して記述することができる」
「ドハティネットワークの超幾何学シンプレックスは、プランクスケール、サブプランクスケール、宇宙論的スケールのシステムとネットワークの進行を示すものである。ドハティネットワークは、ビルケランド電流と呼ばれるフォースフリー場に整列した電流の形状を記述している。ビルケランド電流内の複雑な細部はすべて、コミュニケーション構造に内在する情報の因果的形成を生じさせる形状パワーとして作用する」……それは「フィラメントとノード内の投影動的スケール対称性の幾何学的構造」
「磁気圏のトロイダル磁場と全ての球状天体またはプラネタロイド(小惑星)のそれを作り出す全てのビルケランド電流の根底には再帰的自己相似異径ブルーワール(青い渦)が存在する」
「スコット博士は、ドハティーセットが、フォースフリー場に整列した電流のベッセル関数という彼のモデルと一致し、さらに一歩進んで、彼のモデルが予測する電流の内部の複雑な細部を全て浮き彫りにしていると述べた。彼は文字通り、TDS(The Doherty Set)はまるでビルケランド電流の内側に立って、周りの複雑なディテールをすべて見ることができるかのようだと言った!」
「TDNは、ビルケランド電流のベッセル関数で振動するアノード、カソードの情報パケットを示す! それは完全にその全体が指数関数またはオイラー数であり、それはまた、視覚的に2の平方根であるマップ。TDSは文字通り、宇宙定数、または逆二乗則のメートル法なのだ!」
「TDSは、対数スケール不変でありながら、ヘテロダイナミック再帰的縦波ファイ波埋め込みである! 簡単に言えば、効率、最小抵抗の経路、希薄化に基づいて開閉する穴の幾何学である」
「TDSは実数線の球状積み重ねである。粒子と質量の比を対数スケールで表したものだ。ピエゾ電気結晶格子、内部空間は情報パケット、統合情報プラズモイド!」
「ドハティセットのシステム全体は位相共役にロックされており、それは黄金平均比スケーリングの完全な圧縮であることを意味する! TDSは生きている動的な幾何学で、私たちが身体と呼ぶ様々な大きさの容器の中に生命を封じ込めることができる。生命はこれらすべてのコンテナの中をシームレスに移動する。TDSは、ダイナミックなシステムのスケーラブルな生きた幾何学と言えるかもしれない。さらに、TDSは、生命システムの代謝率やネットワークにおける持続可能性の3/4スケーリング則に合致している。つまり、チューブダイナミクス、コボーディスムなのである。これは、リヒテンベルグパターンと呼ばれる分岐流システムと同じものだ。このパターンは、どんなシステムでも、圧力がかかったり解放されたりすると、必ず出てくる!」
「すべての生物は、私たちが #sonobiology と呼ぶプロセスで、The Dougherty Set [TDS] から音響的に共鳴し、あなたの内側のオルガネラと外側のオルガネラはすべて、TDSで作られたフラクタルフィールドでもある。あなたの腎臓、胚、生命、睾丸、あなたの脳、すべてがソニックジェネシスである」……「魂、精神、アストラルトラベルを含むすべての存在は、まったく同じジオメトリを使用して存在に入り、出て行く。すべてのシステムは、同じ普遍的な超幾何学、すなわちTDSを使って開閉する。TDSは、単純な波動の幾何学を使って、複雑な出現の科学を表現している。建設的・破壊的な波の干渉が、私たちの生きる現実を生み出している」
最後までお読みいただき、ありがとうございました。